问几道自主招生竞赛级别的题目

271828

1.   给定正数$n(n>2)$, 记 $f(n)$ 为集合$\{1,2,\cdots,2^n-1\}$ 的满足如下两个条件的子集$A$ 的元素个数的最小值.
(a)$1\in A, 2^n-1\in A$; (b)$A$ 中的元素(除1外)均为$A$ 中的另两个(可以相等)元素的和。
(1)求 $f(3)$ 的值
(2)求证: $f(100)\leq 108$

2.   若集合$A\subseteq N^*$ 满足(1)$A$ 中的元素个数不小于3; (2)若$a\in A$, 则$a$ 的所有正因子也都属于$A$; (3)若$1<a<b, a,b\in A$, 则$1+ab\in A$.
求证: (1)$\{1,2,3,4,5\}\subseteq A$;  (2)$2014\in A$

3.  同时满足$1+x^4\leq 2(y-z)^2,1+y^4\leq 2(z-x)^2,1+z^4\leq 2(x-y)^2$ 的三元数组$(x,y,z)$ 的个数为多少？

kuing

第3题：由均值有
\[2(y-z)^2\geqslant1+x^4\geqslant2x^2 \riff (y-z)^2\geqslant x^2 \riff (x+y-z)(x-y+z)\leqslant0,\]
同理有另外两式，三式相乘得
\[(-x+y+z)^2(x-y+z)^2(x+y-z)^2\leqslant0,\]
故此三个因式中至少一个为 $0$。
如果 $-x+y+z=0$，则有 $1+y^4=2y^2$, $1+z^4=2z^2$，即 $y=\pm1$, $z=\pm1$，且 $1+(y+z)^4\leqslant2(y-z)^2$，故当 $y=1$ 时 $z=-1$, $x=0$，当 $y=-1$ 时 $z=1$, $x=0$。
另外两种情况同理，故共六个。

kuing

第2题：（1）由条件2知 $1\in A$；

假如 $A$ 中全为奇数，则由条件1知一定存在奇数 $a$, $b$ 且 $1<a<b$，此时 $1+ab$ 为偶数，矛盾，故 $A$ 中必有偶数，所以 $2\in A$；

假如 $3\notin A$，则由条件2知 $A$ 中的所有元素都为 $3k+1$ 或 $3k+2$ 的形式，其中 $k\in\Bbb N$。如果 $c>1$ 且 $c=3k+1$，则由 $2\in A$ 及条件3知 $1+2c=3(1+2k)\in A$，得 $3\in A$，故此除了 $1$ 外全是 $3k+2$ 的形式，由条件2知，这些元素的所有正因子也都要全是 $3k+2$ 的形式，又易知这些元素不会全是质数，于是存在合数 $3k+2$ 能分解为 $ (3k_1+2)(3k_2+2)$，其中 $k_1$, $k_2\in\Bbb N$，展开知矛盾，所以 $3\in A$。

由 $2$, $3\in A$ 得 $2\times3+1=7\in A$, $2\times7+1=15\in A$, $5\in A$, $3\times5+1=16\in A$, $4\in A$。

综上知 $\{1,2,3,4,5\}\subseteq A$；

（2）由 $2014=1+33\times61=1+(1+2\times16)\times(1+4\times15)$ 及前面的过程知 $2014\in A$。

realnumber

第一题目1）穷举如下集合A可以是{1，2，3，4，7},或{1，2，3，6，7},或{1，2，4，6，7}或{1，2，3，5，7}，或{1,2,4,5,7}即$f(3)=5$.


没达到要求，
2)这样的集合符合两条，
如下B={$1,2^1,2^2,2^3....,2^{98},2^{99},2^2-1,2^3-1....,2^{98}-1,2^{99}-1,2^{100}-1$}共有元素199个.只说明$f(100)\le 199$

-----百度搜索到的     2012上海市高中数学竞赛
wenku.baidu.com/link?url=v-Feu3U7QNA8AI4HKgz9 … zpLXQNktEH7IxQWIMdNS

hbghlyj

realnumber 发表于 2014-2-15 14:30
百度搜索到的
2012上海市高中数学竞赛(新知杯)试卷及答案

2012上海市高中数学竞赛（新知杯）试卷

【说明】解答本试卷不得使用计算器

一、填空题（本题满分60分，前4题每小题7分，后4小题每小题8分）

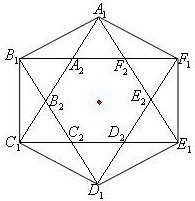
1．如图，正六边形$A_{1} B_{1} C_{1} D_{1} E_{1} F_{1}$的边长为1，它的6条对角线又围成一个正六边形$A_{2} B_{2} C_{2} D_{2} E_{2} F_{2}$，如此继续下去，则所有这些六边形的面积和是 ．

2．已知正整数$a_{1}, a_{2}, \cdots, a_{10}$满足：$\frac{a_{j}}{a_{i}}>\frac{3}{2}, 1 \leq i<j \leq 10$，则$a_{10}$的最小可能值是 ．

3．若$\tan \alpha+\tan \beta+\tan \gamma=\frac{17}{6}$，$\cot \alpha+\cot \beta+\cot \gamma=-\frac{4}{5}$，$\cot \alpha \cot \beta$ $+\cot \beta \cot \gamma$$+\cot \gamma \cot \alpha$

$=-\frac{17}{5}$，则$\tan (\alpha+\beta+\gamma)=$ ．

4．已知关于$x$的方程$\lg (k x)=2 \lg (x+1)$仅有一个实数解，则实数$k$的取值

范围是 ．

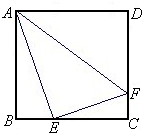
5．如图，$\triangle A E F$是边长为$x$的正方形$A B C D$的内接三角形，已知$\angle A E F=90^{\circ}$，

$A E=a, E F=b, a>b$，则$x=$ ．

6．方程$2^{m} \cdot 3^{n}-3^{n+1}+2^{m}=13$的非负整数解$(m, n)=$ ．

7．一个口袋里有5个大小一样的小球，其中两个是红色的，两个是白色的，一个是黑色的，依次从中摸出5个小球，相邻两个小球的颜色均不相同的概率是 ．（用数字作答）

8．数列$\left\{a_{n}\right\}$定义如下：$a_{1}=1, a_{2}=2, a_{n+2}=\frac{2(n+1)}{n+2} a_{n+1}-\frac{n}{n+2} a_{n}, n=1,2, \cdots$.若$a_{m}>2+\frac{2011}{2012}$，则正整数$m$的最小值为 ．

二、解答题

9．（本题满分14分）如图，在平行四边形ABCD中，$A B=x$，$B C=1$，

对角线AC与BD的夹角$\angle B O C=45^{\circ}$，记直线AB与CD的距离为$h(x)$．

求$h(x)$的表达式，并写出x的取值范围．

10．（本题满分14分）给定实数$a>1$，求函数$f(x)=\frac{(a+\sin x)(4+\sin x)}{1+\sin x}$的最小值．

11．（本题满分16分）正实数$x, y, z$满足$9 x y z+x y+y z+z x=4$；

求证：（1）$x y+y z+z x \geq \frac{4}{3}$；（2）$x+y+z \geq 2$．

12．（本题满分16分）给定整数$n(\geq 3)$，记$f(n)$为集合$\left\{1,2, \cdots, 2^{n}-1\right\}$的满足如下两个条件的子集A的元素个数的最小值：①$1 \in A, 2^{n}-1 \in A$；②A中的元素（除1外）均为A中的另两个（可以相同）元素的和．

（1）求$f(3)$的值；

（2）求证：$f(100) \leq 108$．

2012上海市高中数学竞赛（新知杯）参考答案

1、$\frac{9 \sqrt{3}}{4}$ 2、92 3、11 4、$(-\infty, 0) \cup\{4\}$

5、$\frac{a^{2}}{\sqrt{a^{2}+(a-b)^{2}}}$ 6、$(3,0),(2,2)$ 7、$\frac{2}{5}$ 8、4025

9．解 由平行四边形对角线平方和等于四条边的平方和得

$O B^{2}+O C^{2}=\frac{1}{2}\left(A B^{2}+B C^{2}\right)=\frac{1}{2}\left(x^{2}+1\right)$． ① …………………（2分）

在△OBC中，由余弦定理$B C^{2}=O B^{2}+O C^{2}-2 O B \cdot O C \cos \angle B O C$，

所以 $O B^{2}+O C^{2}-\sqrt{2} O B \cdot O C=1$， ②

由①，②得 $O B \cdot O C=\frac{x^{2}-1}{2 \sqrt{2}}$． ③ …………………（5分）

所以：$S_{A B C D}=4 S_{\triangle O B C}=4 \cdot \frac{1}{2} O B \cdot O C \sin \angle B O C$ $=\sqrt{2} O B \cdot O C$$=\frac{x^{2}-1}{2}$，

故：$A B \cdot h(x)$ $=\frac{x^{2}-1}{2}$， 所以 ：$h(x)=\frac{x^{2}-1}{2 x}$． …………………（10分）

由③可得，$x^{2}-1>0$，故$x>1$．

因为$O B^{2}+O C^{2} \geq 2 O B \cdot O C$，结合②，③可得：$\frac{1}{2}\left(x^{2}+1\right) \geq 2 \cdot \frac{x^{2}-1}{2 \sqrt{2}}$，

解得（结合$x>1$） $1<x \leq \sqrt{2}+1$．

综上所述，$h(x)=\frac{x^{2}-1}{2 x}$，$1<x \leq \sqrt{2}+1$． …………………（14分）

10．解$f(x)=\frac{(a+\sin x)(4+\sin x)}{1+\sin x}=1+\sin x+\frac{3(a-1)}{1+\sin x}+a+2$．

当$1<a \leq \frac{7}{3}$时，$0<\sqrt{3(a-1)} \leq 2$，此时：$f(x)=1+\sin x+\frac{3(a-1)}{1+\sin x}+a+2 \geq 2 \sqrt{3(a-1)}+a+2$，

且当$\sin x=\sqrt{3(a-1)}-1(\in(-1,1])$时不等式等号成立，故$f_{\min }(x)=2 \sqrt{3(a-1)}+a+2$． ………（6分）

当$a>\frac{7}{3}$时，$\sqrt{3(a-1)}>2$，此时“耐克”函数$y=t+\frac{3(a-1)}{t}$在$(0, \sqrt{3(a-1)}]$内是递减，

故此时$f_{\min }(x)=f(1)=2+\frac{3(a-1)}{2}+a+2=\frac{5(a+1)}{2}$．

综上所述，$f_{\min }(x)=\left\{\begin{array}{ll}2 \sqrt{3(a-1)}+a+2, & 1<a \leq \frac{7}{3} \\ \frac{5(a+1)}{2}, & a>\frac{7}{3}\end{array}\right.$ …………………（14分）

11．证 （1）记$t=\sqrt{\frac{x y+y z+z x}{3}}$，由平均不等式：$x y z=(\sqrt[3]{(x y)(y z)(z x)})^{\frac{3}{2}} \leq\left(\frac{x y+y z+z x}{3}\right)^{\frac{3}{2}}$．

…………………（4分）

于是 $4=9 x y z+x y+y z+z x \leq 9 t^{3}+3 t^{2}$，

所以 $(3 t-2)\left(3 t^{2}+3 t+2\right) \geq 0$，

而$3 t^{2}+3 t+2>0$，所以$3 t-2 \geq 0$，即$t \geq \frac{2}{3}$，从而$x y+y z+z x \geq \frac{4}{3}$． …………………（10分）

（2）又因为：$(x+y+z)^{2} \geq 3(x y+y z+z x)$，

所以 $(x+y+z)^{2} \geq 4$，

故 $x+y+z \geq 2$． …………………（16分）

12．解 （1）设集合$A \subseteq\left\{1,2, \cdots, 2^{3}-1\right\}$，且A满足（a），（b）．则$1 \in A, 7 \in A$．由于$\{1, m, 7\}(m=2,3, \cdots, 6)$不满足（b），故$|A|>3$．

又 $\{1,2,3,7\},\{1,2,4,7\},\{1,2,5,7\},\{1,2,6,7\},\{1,3,4,7\},\{1,3,5,7\},\{1,3,6,7\}$

$\{1,4,5,7\},\{1,4,6,7\},\{1,5,6,7\}$都不满足 （b），故$|A|>4$．

而集合$\{1,2,4,6,7\}$满足（a），（b），所以$f(3)=5$． …………………（6分）

（2）首先证明：$f(n+1) \leq f(n)+2, \quad n=3,4, \cdots$． ①

事实上，若$A \subseteq\left\{1,2, \cdots, 2^{n}-1\right\}$，满足（a），（b），且A的元素个数为$f(n)$．

令$B=A \bigcup\left\{2^{n+1}-2,2^{n+1}-1\right\}$，由于$2^{n+1}-2>2^{n}-1$，故$|B|=f(n)+2$．

又$2^{n+1}-2=2\left(2^{n}-1\right), 2^{n+1}-1=1+\left(2^{n+1}-2\right)$，所以，集合$B \subseteq\left\{1,2, \cdots, 2^{n+1}-1\right\}$，且B满足（a），（b）．从而：$f(n+1) \leq|B|=f(n)+2$． …………………（10分）

其次证明：$f(2 n) \leq f(n)+n+1, \quad n=3,4, \cdots$． ②

事实上，设$A \subseteq\left\{1,2, \cdots, 2^{n}-1\right\}$满足（a），（b），且A的元素个数为$f(n)$．

令$B=A \cup\left\{2\left(2^{n}-1\right), 2^{2}\left(2^{n}-1\right), \cdots, 2^{n}\left(2^{n}-1\right), 2^{2 n}-1\right\}$，

由于 $2\left(2^{n}-1\right)<2^{2}\left(2^{n}-1\right)<\cdots<2^{n}\left(2^{n}-1\right)<2^{2 n}-1$，

所以$B \subseteq\left\{1,2, \cdots, 2^{2 n}-1\right\}$，且$|B|=f(n)+n+1$．

而$2^{k+1}\left(2^{n}-1\right)=2^{k}\left(2^{n}-1\right)+2^{k}\left(2^{n}-1\right), k=0,1, \cdots, n-1$， $2^{2 n}-1=2^{n}\left(2^{n}-1\right)+\left(2^{n}-1\right)$，

从而B满足（a），（b），于是：$f(2 n) \leq|B|=f(n)+n+1$． …………………（14分）

由①，②得 $f(2 n+1) \leq f(n)+n+3$． ③

反复利用②，③可得$f(100) \leq f(50)+50+1 \leq f(25)+25+1+51$

$\leq f(12)+12+3+77 \leq f(6)+6+1+92$

$\leq f(3)+3+1+99=108$． …………………（16分）