继续收集数列型的不等式水母

kuing

承接旧版论坛的这个贴 kkkkuingggg.haotui.com/thread-1065-1-1.html ，在这里我们继续来收集类似的数列型的不等式水母。

刚才在某教师群看到的一题：

普宁苏(1035******) 20:37:23
求助

熟知 $f(x)=\ln x/x$ 在 $(0,e)$ 递增，在 $(e,+\infty)$ 递减，故 $\ln x/x\leqslant 1/e$，故此
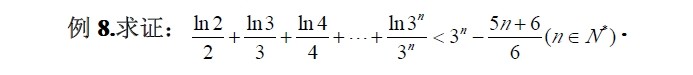
\[\frac{\ln 2}2+\frac{\ln 3}3+\frac{\ln 4}4+\cdots +\frac{\ln 3^n}{3^n}<(3^n-1)\frac1e<\frac{3^n-1}2,\]
因此欲证原不等式只需证
\[\frac{3^n-1}2<3^n-\frac{5n+6}6,\]
即
\[3^n>\frac{5n}3+1,\]
而显然有
\[3^n=(1+2)^n\geqslant 1+2n>\frac{5n}3+1,\]
得证。

kuing

爱好者—520maths(9802*****)  0:25:24


爱好者-战巡(3705*****)  0:33:51
这不是开玩笑吧....

左边>1/ln(2)>1>右边...

realnumber

可以下结论了，高中出现的数列不等式，如果有lnn,什么的，大多是水母~~
2楼又是水母中的水母.

kuing

旧版论坛的这道：kkkkuingggg.haotui.com/thread-999-1-5.html，求证
\[1+\frac12+\frac13+\cdots+\frac1n\geqslant \frac12\ln\frac{(2e)^n}{n!}.\]

不算很水，但还是有点小水，至少从左边无\界而右边有界可以看出来。

当 $n=1$, $2$ 时显然成立；
当 $n=3$ 时右边$=0.5\ln(4e^3/3)=1+1/2+0.5\ln(4/3)<1+1/2+0.5(4/3-1)<1+1/2+1/3$，也成立；
当 $n\geqslant4$ 时，由 $2.5<e<3$ 容易证明 $n! \geqslant 5!\cdot(2e)^{n-5}$，故
\[\frac12\ln\frac{(2e)^n}{n!}\leqslant \frac12\ln\frac{(2e)^5}{5!}<\frac12\ln\frac{2^5\cdot3\cdot e^4}{5!}<\frac12\ln e^4=2,\]
而 $1+1/2+1/3+1/4=25/12>2$，从而不等式成立。

kuing

旧论坛的这道 kkkkuingggg.haotui.com/thread-1402-1-2.html 也收了吧

已知$a_1=1/3$, $a_{n+1}=a_n+a_n^2/n^2$，求证：（1）$a_n<a_{n+1}<1$；（2）$a_n>1/2-1/(4n)$

水的是第2问，因为 $a_4=30760/59049>1/2$

kuing

kkkkuingggg.haotui.com/thread-992-1-1.html

这个虽然是级数，不过其实也是数列型不等式水母而且是大大的水……

realnumber

回复 6# kuing
每一项小于$\frac{1}{\sqrt{2}^nn^2}$,而小于$\frac{1}{n^a},a为大于１的常数$或小于$\frac{1}{a^n},a为大于１的常数$就收敛了．

kuing

又来了
湖北部分重点高中2015届高三第一次联考理数，最后一题：


第三问，尼玛出题的真是太逗了：
\begin{align*}
\text{左边}&\geqslant 4\left(\frac12+\frac23+\cdots+\frac n{n+1}\right)\\
&\geqslant 4\left(\frac12+\frac12+\cdots+\frac12\right)\\
&=2n.
\end{align*}

第一章

你们都善于从菊部发现问题。
我们老师天天告诫：要从全菊把握。

isee

又来了
湖北部分重点高中2015届高三第一次联考理数，最后一题：


第三问，尼玛出题的真是太逗了：
\begin{ ...
kuing 发表于 2014-10-11 15:18

哈哈，出题人可能计上心来被 ln 绕糊涂了

kuing

回复 10# isee

绕糊涂也没啥，糊涂事常有，但如果命题者及至整个命题组对出好的题目认真地重新审视一下，应该很容易发现这个水母。
另外，据说这套题目的第6题是错题。

kuing

突然想起前些天在某教师群也见过一个，忘了贴上来，现补上。

河源张老师(1837****) 15:26:34

广州邓Sir.(9022***) 15:31:42
这个不等式哪里来的？好像是一个很弱的不等式
原题是这样吗？
河源张老师(1837****) 15:31:55
是，

群里的讨论懒得贴了，因为实在太弱：当 $n = 2$, $3$ 时直接验证，当 $n\geqslant 4$ 时，因为显然 $\lg n < n+1$ ，所以 $\text{左边} < n-1 \leqslant \text{右边}$。

kuing

forum.php?mod=viewthread&tid=3276（III）

kuing

2015届高三上学期珠海期末考试理科数学压轴题


分析见 blog.sina.com.cn/s/blog_6dc68ba80102vg32.html

其实后面还可以写得简洁些，直接 左边 $>\dfrac m{\ln(m+1)}(m+n)>m+n>n$ 就行，水母中的水母

kuing

水母（III）当 $n=1$, $2$ 时自行验证，当 $n\geqslant3$ 时，熟知 $\ln2\approx 0.693$，故 $\ln2+\ln4=3\ln2>2$，所以 $\ln2+\ln3+\ln4+\cdots+\ln(n+1)>n$，故只需证 $10n(n+1)\geqslant 9n^2+4n$，显然成立。

realnumber

弱弱的“水母”不等式继续出现，还是有不少人不知道啊~~~

kuing

渝X教师多多<a1814**********com> 10:18:40

粤A爱好者战巡(3705*****) 10:23:05
你不觉得右边是个很小的量么
右边的最大值连1都远远没到
而且对于越大的n来说，右边干脆就是负的
豫U教师张琦(3289*****) 10:25:03
右端就是负的，n是正整数
粤A爱好者战巡(3705*****) 10:25:51
又可以加入渣k的水母不等式

色k

浙C教师第15年(1746******) 2015-11-27 19:04:01


kuing(249533164) 2015-11-27 19:11:34
目测是水母
bn 那么大的数量级，f(n) 就更大了

kuing(249533164) 2015-11-27 19:19:33
显然 bn >=2 所以 f(n) 一定大于 5^n，于是左边 < 1/5+1/5^2+...  <1/4

kuing(249533164) 2015-11-27 19:21:23
你看，只用 >=2 就已经能水出来了，跟实际上还差很远
水成这样也是难得一见的

川X教师咪哆<liuzj288*********com> 2015-11-27 19:24:54
多水

kuing

辽B爱好者1bk3(2047******) 23:27:34

请各位帮忙看看，最后这个不等式左端直接小于n，右端直接大于n，还用得着证明吗？
豫N学生一铭(2770*****) 23:32:07
都水成啥了
辽B爱好者1bk3(2047******) 23:33:40
这还是“东北三省四市教研联合体高考模拟（一）数学（理）试题”，我都怀疑是不是真的
阅A爱好者渣k(249533164) 0:50:06
又见超级大水母

kuing

茂名一中刘海霞(7821*****) 22:26:56

麻烦各位帮我看看最后一步
最后那个式子是怎样计算出来的呢

广州郭子伟(kuing)(249533164) 22:57:29
原不等式是水母啦，没必要数归
当 n=3 时易知成立；
当 n>=4 时，
左边 >= (1+2+...+n)(1+1/2+1/3+1/4) > n(n+1) > 右边