来自粉丝群“发错地方”的椭圆题

kuing

第一章  13:22:07

发错地方
kuing  13:33:40
哪的题？
第一章  13:35:36
不知道、。
第一章  13:36:48
老齐那边的题。
那个苏州教研员陈兆华，可能是自己发现的吧。
他说他自己证不了
kuing  13:37:24
我用极点极线再拉成圆可以证明出来
第一章  13:37:41
就知道你伸缩
kuing  13:38:30
伸缩前要先用极点极线证明一个共线，然后才好伸缩
顺便也得到了推广结论
F和准线可以换成点和相应极线
第一章  13:39:04
我也猜想极点极线，不过没动手。
估计也做不了
就是这个不懂
上班打卡先

连结 $AN$ 交椭圆于 $D$，如图所示



因为 $MN$ 实际上是椭圆关于 $F_2$ 的极线，所以 $BD$ 必过 $F_2$。

连结 $BD$，然后作伸缩变换，延 $y$ 轴方向，将椭圆拉伸成圆（注意 $F_1$, $F_2$ 及准线都是不变的），如图所示



由于 $A'B'$ 为圆的直径，于是显然 $F_2$ 是 $\triangle A'B'N'$ 的垂心，所以 $N'F_2\perp A'B'$，即 $k_{N'F_2}\cdot k_{A'B'}=-1$。

另一方面，我们假设椭圆方程为 $x^2/a^2+y^2/b^2=1$ 其中 $a>b>0$，则上述伸缩变换为 $y\to ay/b$，此时所有直线的斜率将由 $k$ 变为 $ak/b$，代入上述结论即得变换前有
\[\frac abk_{NF_2}\cdot\frac abk_{AB}=-1,\]
即
\[k_{AB}\cdot k_{F_2N}=-\frac{b^2}{a^2}.\]

abababa

所以$BD$必过$F_2$，这个能请版主详细证明一下吗？我对极点、极线这方面的东西没什么基础，网友给我讲过一些，我只学习了一个“极线1上一点的极线2必过极线1的极点”这个定理。
还有版主之前说的有一般的情况，能请详细证明一下吗？

转化与化归

回复 1# kuing
我就老老实实的证吧！

易证 $k_{C B} \cdot k_{C A}=-\frac{b^2}{a^2}, \because k_{C A}=\frac{y_1}{x_1-c}, \quad \therefore k_{C B}=-\frac{b^2}{a^2} \cdot \frac{x_1-c}{y_1}$,
\[
k_{F_2 N} \cdot k_{A B}=\frac{k_{C B}\left(\frac{a^2}{c}+x_1\right)-y_1}{\frac{b^2}{c}} \cdot \frac{y_1}{x_1}=\frac{-\frac{b^2}{a^2} \cdot \frac{x_1-c}{y_1}\left(\frac{a^2}{c}+x_1\right)-y_1}{\frac{b^2}{c}} \cdot \frac{y_1}{x_1}=\frac{c}{b^2} \cdot \frac{-\frac{b^2}{a^2}\left(x_1-c\right)\left(\frac{a^2}{c}+x_1\right)-y_1^2}{x_1}
\]
\[
=\frac{c}{b^2} \cdot \frac{-b^2\left(\frac{x_1^2}{a^2}+\frac{y_1^2}{b^2}-1\right)-\frac{b^4}{a^2 c} x_1}{x_1}=-\frac{b^2}{a^2}
\]

abababa

请教了一位网友，把那个共线的证明了，但看起来觉得挺难的，绕着绕着就迷糊了

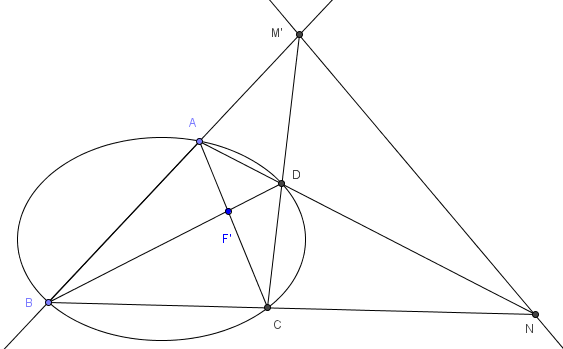
设$AC,BD$交于$F'$，$AB,CD$交于$M'$，于是$\triangle F'M'N$自极，$N$的极线为$F'M'$
因为$F'$的极线为$M'N$过点$N$，所以$N$的极线过点$F'$
因为$F$的极线为$MN$过点$N$，所以$N$的极线过点$F$
假设$F,F'$不重合，于是$N$的极线为$FF'$，即为$AC$
于是$N$的极线既为$F'M'$又为$AFF'C$，所以$M'$在$AC$上
于是$AB,CD,AC$共点于$M'$，但$AB,AC$共点于$A$，于是$M',A$重合
于是$CD$交$AB$于$A$交椭圆于$D$，但$A$在椭圆上，于是$A,D$重合
于是$AB,CD$的交点$F'$即为点$A$，$F'$的极线$M'N$即为切线$AN$
于是$N$的极线过点$A$，但$N$的极线又过点$F$，于是$N$的极线为$AF$，而$F$在$AC$上，所以$AF$与$AC$重合，即$N$的极线为$AC$
由于$AN$与椭圆相切，所以$BCN$与椭圆相切，即$B,C$重合
于是$BD$即为$AC$，而$F$在$AC$上，所以$F$也在$BD$上
若$F,F'$重合，则显然$BFD$共线，此时$F'$的极线$M'N$即为$F$的极线$MN$，于是$M$为$AB,CD$的交点，所以$CDM$也共线

isee

回复 1# kuing

今天这道题，第一次用坐标伸缩变换角度自己写了下。

如图1所示，在平面直角坐标系$xOy$中，椭圆$E:\dfrac {x^2}{a^2}+\dfrac {y^2}{b^2}=1(a>b>0)$的离心率为$\dfrac {\sqrt 2}2$，直线$l:y=\dfrac 12x$与椭圆$E$相交于$A$，$B$两点，$AB=2\sqrt 5$，$C$，$D$是椭圆$E$上异于$A$，$B$两点，且直线$AC$，$BD$相交于点$M$，直线$AD$，$BC$相交于点$N$.       
        （1）求$a$，$b$的值；       
        （2）求证：直线$MN$的斜率为定值.




做法与楼主基本一样，
由（2）知，只要AB弦过椭圆的中心均有此结论。（三对垂直，三对斜率积等，图形上也好看。。。）