相传的某校自招题

guanmo1

非联盟类的高校。

战巡

回复 1# guanmo1


其他的就不吐槽了，第一题尼玛就是错的.......
\[\sum_{n=1}^{2014}\frac{1}{2n-1}>\int_{1}^{2015}\frac{dx}{2x-1}=\frac{\ln(1+2·2014)}{2}\approx 4.15\]

tommywong

1+1/3+1/5+...+1/15=2.02...

guanmo1

回复 3# 战巡


    看到的手写帖子，要么是写错了，分母是2的n次方减1？

guanmo1

第2,3,4题呢

踏歌而来

回复 5# guanmo1
确实是2^n-1。

kuing

第二题你没发现（1）（3）是一样的么？……结果就没答案了，因为答案就是丢了的那个

\[AG^2=\frac19\bigl(\vv{AB}+\vv{AC}\bigr)^2 =\frac19(b^2+c^2+2bc\cos A)=\frac19(2b^2+2c^2-a^2),\]
故
\begin{align*}
GA^2+GB^2+GC^2>\frac83R^2 &\iff a^2+b^2+c^2>8R^2 \\
&\iff\sin^2A+\sin^2B+\sin^2C>2 \\
&\iff\sin^2A-\cos^2B-\cos^2C>0 \\
&\iff-\cos(A-B)\cos(A+B)-\cos^2C>0 \\
&\iff\cos C\bigl(\cos(A-B)+\cos(A+B)\bigr)>0 \\
&\iff2\cos A\cos B\cos C>0.
\end{align*}

战巡

回复  guanmo1
确实是2^n-1。
踏歌而来 发表于 2014-3-3 18:58

这样的话可就是烂题一道了...
\[\frac{1}{2^n-1}-\frac{1}{2^{n-1}}=-\frac{2^n-2}{2^n(2^n-1)}\le 0\]
\[\sum_{n=1}^{2014} \frac{1}{2^n-1}<\sum_{n=1}^\infty \frac{1}{2^n-1}\le \sum_{n=1}^\infty \frac{1}{2^{n-1}}=2\]

战巡

回复 1# guanmo1

第三题，如图

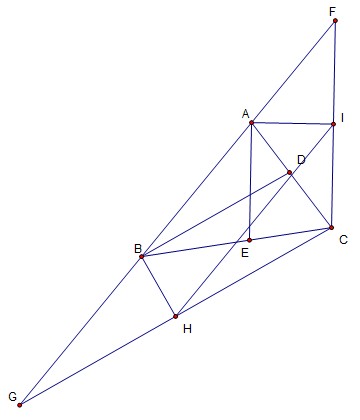
$AE, BD$为角平分线，$CF∥AE, CG∥BD, BH⊥CG, AI⊥CF$
显然$∠BCH=\frac{B}{2}, ∠ACI=\frac{A}{2}$
加上两个垂直，有$CH=BC\cos(\frac{B}{2})=a\cos(\frac{B}{2}), CI=AC\cos(\frac{A}{2})=b\cos(\frac{A}{2})$
又易证$∠ICH=C+\frac{A}{2}+\frac{B}{2}, \cos(∠ICH)=\cos(C+\frac{A}{2}+\frac{B}{2})=\cos(\frac{C}{2}+90\du)=-\sin(\frac{C}{2})$
然后余弦定理得
\[HI^2=CH^2+CI^2-2\cos(∠ICH)·CH·CI=a^2\cos^2(\frac{B}{2})+b^2\cos^2(\frac{A}{2})+2ab\cos(\frac{A}{2})\cos(\frac{B}{2})\sin(\frac{C}{2})\]
又易证$BC=BG, AC=AF$，可知$H, I$为$CG, CF$中点，$HI=\frac{FG}{2}=\frac{BG+AB+AF}{2}=\frac{BC+AB+AC}{2}=1$
\[a^2\cos^2(\frac{B}{2})+b^2\cos^2(\frac{A}{2})+2ab\cos(\frac{A}{2})\cos(\frac{B}{2})\sin(\frac{C}{2})=1^2=1\]

kuing

回复 9# 战巡

刚才躺床上想到了这个，起来刚画好图……刷新就看到一样的……

guanmo1

回复 8# 战巡


    如果是2^n-1话，确实没意思了。

guanmo1

第4题画图像有想法吗

战巡

回复 12# guanmo1

我是倾向于无视这种题目...没啥严谨性可言，反正手绘，差不多就行了

三次曲线，果断九点法完爆啊...
就是随便列9个满足方程的点，用平滑曲线连起就差不多了，至于这9个点的位置，不用太仔细，估算就好了

kuing

\[AG^2=\frac19\bigl(\vv{AB}+\vv{AC}\bigr)^2 =\frac19(b^2+c^2+2bc\cos A)=\frac19(2b^2+2c^2-a^2),\]
故
\begin{align*}
GA^2+GB^2+GC^2>\frac83R^2 &\iff a^2+b^2+c^2>8R^2 \\
&\iff\sin^2A+\sin^2B+\sin^2C>2 \\
&\iff\sin^2A-\cos^2B-\cos^2C>0 \\
&\iff-\cos(A-B)\cos(A+B)-\cos^2C>0 \\
&\iff\cos C\bigl(\cos(A-B)+\cos(A+B)\bigr)>0 \\
&\iff2\cos A\cos B\cos C>0.
\end{align*}
kuing 发表于 2014-3-3 19:30

$\sin^2A+\sin^2B+\sin^2C>2$ 之后还可以像这样玩 bbs.pep.com.cn/forum.php?mod=redirect&got … 5441&pid=6564597

其妙

我都觉得在人教哪里玩过，找不到了