下午在人教群看到的“安徽竞赛最后一题”

kuing

教师-小农(4310***) 14:59:36

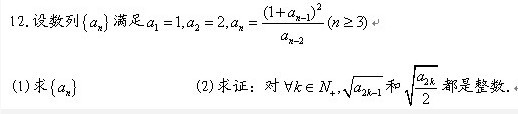
教师-小农(4310***) 15:00:05
发个数列题目，安徽竞赛最后一题，只有答案。没有过程

话说，解答题又怎么会“只有答案。没有过程”？真怪，不管它了，玩玩看。

前段时间见过类似的递推式，学会了求通项方法，来实践一下：

（1）由递推式得
\begin{align*}
a_na_{n-2}&=(1+a_{n-1})^2 ,\\
a_{n+1}a_{n-1}&=(1+a_n)^2 ,
\end{align*}
相减得
\[a_{n+1}a_{n-1}-a_na_{n-2}=a_n^2+2a_n-a_{n-1}^2-2a_{n-1},\]
显然 $a_n$ 全为正，故整理得
\[\frac{a_{n+1}+a_{n-1}+2}{a_n}=\frac{a_n+a_{n-2}+2}{a_{n-1}},\]
易计算得 $a_3=9$，故
\[\frac{a_{n+1}+a_{n-1}+2}{a_n}=\frac{a_3+a_1+2}{a_2}=6,\]
即
\[a_{n+1}=6a_n-a_{n-1}-2,\]
配凑为
\[a_{n+1}-\frac12=6\left( a_n-\frac12 \right)-\left( a_{n-1}-\frac12 \right), \]
记特征方程 $x^2=6x-1$ 的两根分别为 $\alpha=3+2\sqrt2$, $\beta=3-2\sqrt2$，则易解得
\[a_n=\frac12+\frac{\alpha^{n-1}}4+\frac{\beta^{n-1}}4;\]

（2）对于奇数项，有\[a_{2k+1}=\frac12+\frac{\alpha^{2k}}4+\frac{\beta^{2k}}4=\frac12+\left( \frac{\alpha^k}2+\frac{\beta^k}2 \right)^2-\frac{\alpha^k\beta^k}2=(2a_{k+1}-1)^2,\]
由（1）知 $a_n$ 全为正整数，故奇数项为都完全平方数；

对于偶数项，有
\begin{align*}
\frac{a_{2k}}2&=\frac14+\frac{\alpha \cdot \alpha^{2k-2}}8+\frac{\beta \cdot \beta^{2k-2}}8 \\
& =\frac14+\left( \sqrt{\frac{\alpha }8}\cdot \alpha^{k-1}+\sqrt{\frac{\beta}8}\cdot \beta^{k-1} \right)^2-\frac{\sqrt{\alpha \beta }\alpha^{k-1}\beta^{k-1}}4 \\
& =\left( \sqrt{\frac{\bigl(1+\sqrt2\bigr)^2}8}\cdot \alpha^{k-1}+\sqrt{\frac{\bigl(1-\sqrt2\bigr)^2}8}\cdot \beta^{k-1} \right)^2 \\
& =\left( \frac{2+\sqrt2}4\cdot \alpha^{k-1}+\frac{2-\sqrt2}4\cdot \beta^{k-1} \right)^2,
\end{align*}
令
\[b_k=\frac{2+\sqrt2}4\cdot \alpha^{k-1}+\frac{2-\sqrt2}4\cdot \beta^{k-1},\]
容易验证其满足 $b_1=1$, $b_2=5$ 且 $b_{k+2}=6b_{k+1}-b_k$，所以 $b_k$ 全为正整数，故偶数项的一半亦为完全平方数。

kuing

偶数项那里不知有没有搞复杂了……不知答案怎样

睡神

偶菜鸟想法：先证了第二问，再求第一问…

kuing

回复 3# 睡神
搞出来再说啊……
PS、第二问我开始想的时候也没打算用通项，想从递推式整出平方数的样子，结果没成功，只好老实用通项……

睡神

噢…应该能搞出啪…最近脑袋装满了花岗岩，没细胞想题…

kuing

回复 5# 睡神
慢慢来，等你的妙解

Tesla35

猜对了。。。。。。。

Tesla35

回复 7# Tesla35
这类题证明是整数、是完全平方数都是一个方法：证明是线性递归数列。。。（平方的只需证明数列每一项的算术平方根是线性递归数列即可）。。
下面只证奇数项的，偶数项同理。。
暴力计算前几项：
$a_1=1,a_2=2$
$a_3=3^2,a_4=50$
$a_5=17^2,a_6=1682$
$a_7=99^2,a_8=57122$
……
好了，猜想${a_n}$的奇数项的算术平方根构成线性递归数列
设$\sqrt{a_{2k+1}}=p\sqrt{a_{2k-1}}+q\sqrt{a_{2k-3}}$
有：
$3p+q=17,17p+q=99$
计算得：
$p=6,q=-1$
因此：
$\sqrt{a_{2k+1}}=6\sqrt{a_{2k-1}}-\sqrt{a_{2k-3}}$
已验证此递推式对于$a_9$是正确的。
想办法证明即可。。（数归，或者肯定有直接方法）。。交给大家了

Tesla35

回复 1# kuing


    哦哦。没仔细看kk的

Tesla35

会了。。
受kk启发
$a_{n+1}=6a_n-a_{n-1}-2$
$a_na_{n-2}=(1+a_{n-1})^2$得
$\sqrt{a_na_{n-2}}=1+a_{n-1}$下标加2
$\sqrt{a_{n+2}a_{n}}=1+a_{n+1}$
上面两式相加得：
$\sqrt{a_na_{n-2}}+\sqrt{a_{n+2}a_{n}}=2+a_{n-1}+a_{n+1}=6a_n$
立得：$\sqrt{a_{n-2}}+\sqrt{a_{n+2}}=6\sqrt{a_n}$
下略

爪机专用

回复 10# Tesla35

soga, very nice!
果然我又做复杂了

Tesla35

网上的解答

kuing

回复 12# Tesla35

怎么得出的？

Tesla35

上个全图
用了通项

其妙

都喜欢命制这种题，那个东南刚刚过，这道也来了。
不过伪装了一下，加了个常数的尾巴。
共性都是那个递推公式，只是前两项不同。

kuing

回复 14# Tesla35

汗，没变形过程，这也能算答案？

零定义

看看...先f掉第二问，在f第一问，是可行的D...