|
|
original poster
isee
posted 2014-4-25 01:19
证明,如图
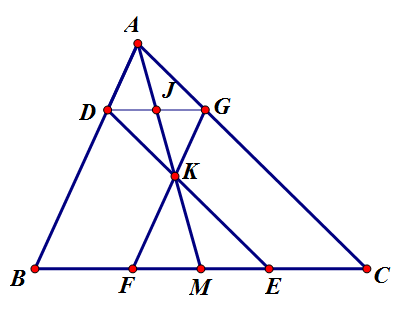
记DE与FG相交于K,连接AK,延长线交BC于M。
由于DE与FG均平分三角形ABC的面积,于是
\[\frac {BD}{BA}=\frac {1}{\sqrt 2}=\frac {CG}{AG} \Rightarrow DG\sslash BC\]
而平行四边形ADKG,$DJ=JG$,于是
\[\frac {DJ}{ME}=\frac {JG}{MF}\Rightarrow FM=ME\]
另一方面 \[DG\sslash BC,S_{\triangle DBE}=S_{\triangle GFC}\Rightarrow BE=FC\]
从而,M为BC中点,得证。 |
|