在中考范围内用柯西……(2014年5月海淀中考数学一模)

isee

2014年5月海淀中考数学一模，第25题，另类解法。
我真的觉得，这题如果放在高二，只考第三问，不知道得分率如何（普通班）。


自己汗一个，高考范围内，好像只用过那么一两回。






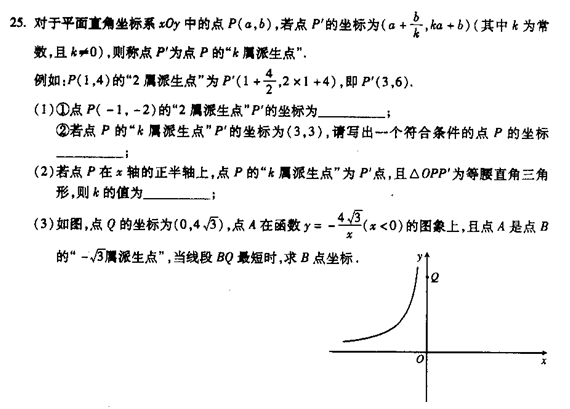
第3问，解：

设$B(x,y)$，则$A(x+\dfrac y{-\sqrt 3},-\sqrt 3 x+y)$，依题设有
\[x+\frac y{-\sqrt 3}<0\Rightarrow \sqrt 3 x-y<0\]

于是：
\begin{align*}
\left(x+\dfrac y{-\sqrt 3}\right) \cdot \left(-\sqrt 3 x+y\right)&=-4\sqrt 3\\
\left(\sqrt 3 x-y\right)^2& =12\\
\Rightarrow \sqrt 3 x-y&=-2\sqrt 3\tag{1} \label{eq02}\\[2ex]
BQ^2=(x-0)^2+(y-4\sqrt 3)^2&=\left((x-0)^2+(y-4\sqrt 3)^2\right)\left((\sqrt 3)^2+(-1)^2\right)\cdot \frac 14\\
&\geqslant \left(\sqrt 3 x-y+4\sqrt 3\right)^2\cdot \frac 14\\
&=\left(-2\sqrt 3+4\sqrt 3\right)^2\cdot \frac 14\\
&=3
\end{align*}

取“=”时
\[\frac x{\sqrt 3}=\frac {y-4\sqrt 3} {-1}\tag{2} \label{eq03}\]

联立\eqref{eq02}\eqref{eq03}式，即得

\[x=\dfrac 32,y=\dfrac {7\sqrt 3}2\]

即\[B\left(\dfrac 32,\dfrac {7\sqrt 3}2\right)\]





＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
顺便问下，题中的坐标变换，有具体对应的几何模型么？

其妙

人家用消元法与二次函数，你用柯西吓唬他们！

isee

回复 2# 其妙


    写得玩玩  不过   真在中考范围内  也不能直接两点距离公式 ……

        不过就图个疼快 了他考试

其妙

回复 3# isee

isee

回复 4# 其妙

论坛里可能有初中生，照顾一下，这些上进的学生吧。

解释一下，这里：\[\left(x^2+(y-4\sqrt 3)^2\right)\left((\sqrt 3)^2+(-1)^2\right)\geqslant \left(\sqrt 3 x-y+4\sqrt 3\right)^2\]


缘于这个因式分解(这里不妨令$abcd\ne 0$)
\begin{align*}
(ac+bd)^2+(ad-bc)^2&=a^2c^2 +2abcd+b^2d^2+a^2d^2-2abcd+b^2c^2\\
&=a^2c^2 +b^2d^2+a^2d^2+b^2c^2\\
&=(a^2+b^2)(c^2+d^2)\\
\therefore   (a^2+b^2)(c^2+d^2)&=(ac+bd)^2+(ad-bc)^2
\end{align*}

于是
\begin{align*}
  (a^2+b^2)(c^2+d^2) \geqslant (ac+bd)^2 \tag{3} \label{eq04}
\end{align*}

取“=”时
\[(ad-bc)^2=0\Rightarrow \frac ac=\frac bd\]

这\eqref{eq04}式，就是柯西(Cauchy)不等式了。

其妙

回复 5# isee
，你实际上把拉格朗日恒等式在$n=2$时证明了一遍吧？