|
|
四面体ABCD中,AB=2,CD=4,且AB⊥CD,又AC+AD=BC+BD=2m(m为常数),求证此四面体在AC=AD=BC=BD时,体积达到最大值.
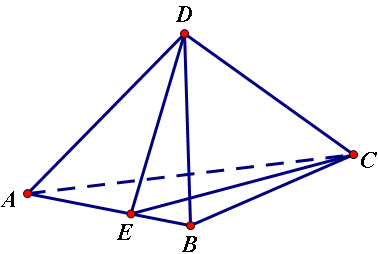
同事韩的设想,完整写出来是这样:作DE垂直AB,交AB于E.连接EC,那么可以证明AB⊥EC.
假设AE>EB,那么AD>BD,AC>BC与AC+AD=BC+BD矛盾.AE<EB,同样有矛盾.所以AE=EB.
接下来说明:在BD=BC=m时,体积最大.
即要使得E到DC的距离最大.作EF垂直CD,交CD于F.EF是BF在面DCE上的射影,如此,当DB=BC时,BF最大,即此时EF最大.
因为由BC+BD=2m,说明B在面BDC的轨迹是椭圆,当B为椭圆的短轴顶点时,B到长轴的距离最大.完(这个做法避开了椭球的说法). |
|