猜想圆与过焦点的直线相切（15楼结论，13楼遗留一题）

kuing

这贴的内容太专业鸟，只能等以后能静下心来时再慢慢品味了……

isee

哈哈，你看我长得像百度吗？

M大太逗了。

kuing

回复 22# isee

abababa

回复 22# isee
回复 22# isee
他是让我用百度去搜索线性代数的书吧，只是看了也没懂，后来我又问了他，这次他给我讲了一个几何证明

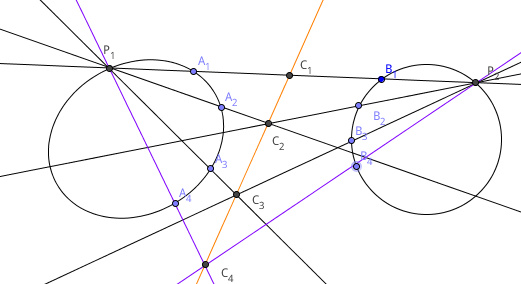
先是讲了一个射影对应，两个二次曲线有三组对应元素确定了，就能确定一个射影对应，作图时先连$A_1B_1$，分别交两个曲线于$P_1$和$P_2$
然后作$P_1A_2$和$P_2B_2$的交点$C_2$，再作$P_1A_3$和$P_2B_3$的交点$C_3$，再作$C_2C_3$和$A_1B_1$的交点$C_1$，这样$A_1,A_2,A_3$就通过轴$C_2C_3$对应到$B_1,B_2,B_3$，对曲线1上的任意一点$A_4$，作$P_1A_4$交轴$C_2C_3$于$C_4$，再作$P_2C_4$和曲线2的交点，就是射影对应中的$B_4$
然后还是像他证明的那样，先证$M,N,F,E$四点共线

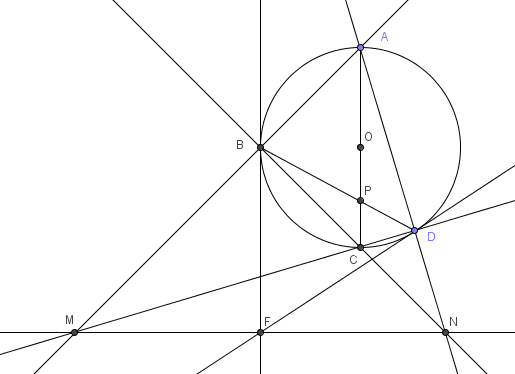
然后他用射影对应把椭圆上的四边形$ABCD$对应到单位圆上，分别让$A,B,C$的坐标是$(0,1),(-1,0),(0,-1)$
$\triangle PMN$是自极三角形,点$P$的极线是$MN$，所以$AC \perp MN$，又因为$BF$是切线，容易证明$BF \sslash AC$，所以$BF \perp MN$
因为$\angle NBF=\angle CAB=45^\circ$，$\angle MBN=90^\circ$，所以$BF$平分$\angle MBN$，这样就有$\triangle BFM \cong \triangle BFN$，所以$FM=FN$
因为过$A,C$的切线的交点$E$是无穷远点，$F$是中点，所以$M,N,E,F$是调和点列

isee

回复 24# abababa


    这帖因为你，更加严谨了。不过，那些证明，都是高等几何的东东，估计能明白的人不多。


其实，这些都可以直接解析几何计算证明的。

谢谢M大，谢谢abababa

isee

回复 25# isee

不知，13楼的平面几何，有没人有兴趣解。偶只是猜测是对的。

abababa

回复 26# isee
13楼的是垂直的，也是他证明的，我只是按他说的用软件算了结果，原理那部分我还没完全理解，以前他也给我讲了很多三线坐标的用法，我都理解得不好

hbghlyj

回复 13# isee

$EH=BH-BE=\frac{AB+BC-AC}2-\frac{AB+BD-AD}2=\frac{BC+AD-AC-BD}2$
同理$DF=\frac{BC+AD-AC-BD}2$
所以EH=DF
∵$I_1H⊥I_2H$∴$△I_1ED\sim △DFI_2$,∴$I_1E·I_2F=ED·DF,$∴$I_1E·I_2F=HF·EH,$∴$△I_1EH\sim △HFI_2$,∴$I_1H⊥I_2H$
所以，以$I_1I_2$为直径的圆与BC的交点是H和D
13楼旁切圆的证明是类似的
等腰三角形的情况见6941的16楼

hbghlyj

△ABC中，AD为角平分线，圆O,O'为ABD,ACD的内切圆，分别切AD于M,N，直线NO,O'M交于P，证明:PA⊥AD
证明：∵OM∥O'N,△AOM~△AO'N,∴AM:AN=OM:O'N=PM:PO',∴PA∥O'N,∴PA⊥AD

△ABC中,E,F是边BC上两点,∠BAE=∠CAF.△ABE,△ACF的内切圆分别与AY,AX切于P,Q两点.证明:两圆根轴平分PQ.
证明：

hbghlyj

圆$I_1,I_2$的另一条外公切线交AB,AC于J,K,PE,QF交于M,JE,KF交于L,JK,AD交于R,则
(1)M为DL中点
(2)DL⊥JK
当D在BC上运动时
(3)AR为定值
(4)L的轨迹为直线

isee

此图作于2014年1月，若改椭圆为圆，则O为三角形PQR的垂心。
isee 发表于 2014-5-23 23:03

源自知乎提问


以下结论的延伸，极线极点，自极三角形



题：圆内接四边形 $ABCD$ 边 $AB,CD$ 所在的直线相交于点 $E,$ $BC,AD$ 相交于点 $F,$ $AC,BD$ 相交于点 $G,$ 求证：圆心 $O$ 点是 $\triangle EFG$ 的垂心.

图 1

如图 1 字母，先证 $OG\perp EF$ 等价于 $GE^2-OE^2=GF^2-OF^2,$ 详尽请移步 定差幂线——引理 1.

引理 2：任一点 $F$ 对半径为 $R$ 的圆 $O$ 的幂为 $FO^2-R^2(=FD\cdot FA>0)$ (在图 1图中.）

另如，在图 1, 圆内点 $G$ 的幂为 $GO^2-R^2(=-(AG\cdot GC)<0)$.

在直线 $FG$ 上取点 $H$ 使

\begin{equation*}FG\cdot FH=FD\cdot FA,\tag{01}\end{equation*}

即 $\color{red}{A,H,G,D}$ 四点共圆，则

\[\angle AHF=180^\circ-\angle ADG=180^\circ-\angle ACB=\angle ACF,\]

所以 $\color{red}{A,H,C,F}$ 四点共圆，所以

\begin{equation*}FG\cdot GH=AG\cdot GC,\tag{02}\end{equation*}

$(01)-(02)$ 整理有 $\color{#f127d2}{GF^2=FD\cdot FA-AG\cdot GC},$ 即 (由引理 2 知)

$$\color{blue}{GF^2=F {~}\text{的幂}{~}+G{~}\text{的幂}}=(FO^2-R^2)+(GO^2-R^2).$$

同理有 $GE^2=$ $E$ 的幂 $+$ $G$ 的幂 $=(EO^2-R^2)+(GO^2-R^2),$

所以

$$GE^2-GF^2=EO^2-FO^2\iff GE^2-OE^2=GF^2-OF^2.$$

由引理 1 知 $OG\perp EF.$ 同样的可证 $OF\perp EG$，即点 $O$ 是 $\triangle EFG$ 的垂心.