圆的证明垂直

乌贼

转人教论坛：bbs.pep.com.cn/forum.php?mod=viewthread&t … =page%3D1&page=4
    如图：已知$P$是圆$O$直径$AB$延长线上一点，且$2PB=AB$，过$P$点作圆的切线，切点为$D$，
过$A$作$AC\perp PD$，垂足为$C$，交圆于$E$，连接$PE$交圆于$F$，连接$AF$并延长交$PC$于
$G$，过$C$作$CH\perp AP$于$H$，连接$EH,GH$。求证：$EH\perp GH$。

乌贼

回复 1# 乌贼
挖挖坟，求简洁几何法。

isee

真早。

这图太复杂了，复杂得看不下去。

isee

原帖4楼 jingling886：“先证△DOB是等边三角形，再证△HEC～△HGP”

原帖18楼 南山菊 ：“$PG^2=GF\cdot GA=DG^2$”，理由在28楼，26楼 秋风树林 “连接BE”，“证明三角形PGF相似于三角形AGP”，再对（GD，GA）“用切割线定理”

于是原帖，18楼 南山菊 ：“$\dfrac{CE}{PG}=\dfrac {2CE}{2PG}=\dfrac {ED}{PD}=\dfrac {OD}{PD}=\tan 30^\circ=\dfrac {CH}{PH}$”

完成原帖4楼 jingling886 方向 得到证明。

简单自然，有什么不好？

isee

反思一下，大众讨论结果，优化即：

连接$BE$，则

\[BE\perp PC\Rightarrow \angle GPF =\angle FEB=\angle FAB=\angle GAP\Rightarrow GP^2=GF\cdot GA=GD^2\Rightarrow GP=GD\]

注意$AB=2BP,OD\perp PC$，连接$BG$，即得矩形$CEBG$，从而

\[\frac {EC}{PG}=\frac {BG}{PG}=\frac {HC}{HP}\]

另一方面，(连接$DB$)，容易证明(正$\triangle DOB\Rightarrow 30^\circ=)\angle HCE=\angle HPG$，（前面括号内为多余的，无需要这个30度角）

于是
\[\triangle ECH \sim HGP\Rightarrow HEC=\angle HGP\]

从而$C,E,H,G$四点共圆，得证。

isee

圆幂定理，现在中考范围内属于高三内容，当然竞赛不限。

除了竞赛（这个竞赛又太简单），已然很少见到这种题了。

乌贼

回复3楼，不是早，是很晚
isee看贴透彻，原来证明$G$为$PD$的中点是这样……
如图，$P$为圆外一点，$PC$为圆切线，$DB//PC$，$PD$交圆于$E$，$AE$延长线平分$PC$。

乌贼

回复 5# isee
若$PG=GD$，可连接$GB$，$\angle BGP=90^circ$，$C,H,B,G$四点共圆，
连接$BE$，$C,E,H,B$四点共圆，有$C,E,H,B,G$五点共圆，得证。

isee

回复 7# 乌贼


    是这样，高中有些练习册里能见到这楼的题。

isee

从高观点下看就是 线段被他的中点和无穷远点调和（调和点列，竞赛里的基础），也因此，这类习题很多。

可惜的是，找了下，没找到以前再哪儿看到的。

补充如下：

单独拿出来，
上图，当有中点与三点在虚线上是等价的，
下图是一般情况，A，B，C，D四点是调和点列。

====
2018年7月16号更新，图应该是snap01才是本题的解释.

椭圆参阅 2018年北京卷文科第20(3)



平D为无穷远点时，即上图中的平行，C就成AB中点了。

乌贼

回复 9# isee
原来是练习题

乌贼

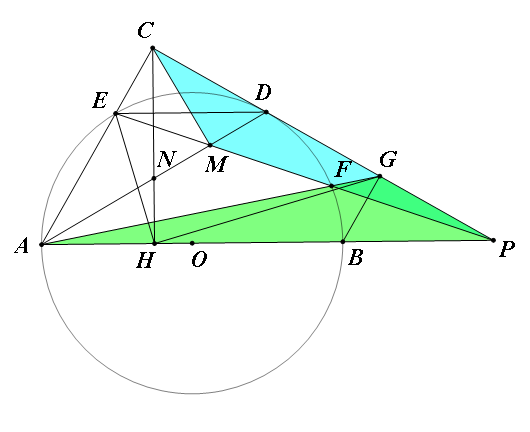
不用圆幂定理，连接$AD$分别交$PE,CH$于$M,N$，连接$ED$。易知$AN=ND,\triangle CND$为正三角形。
$\triangle EDM\sim\triangle PAM\riff\dfrac{AM}{MD}=\dfrac{AP}{ED}=3\riff MN=DM\riff\angle MCD=30^\circ,\dfrac{CM}{CD}=\dfrac{\sqrt3}2$，又$\angle AFE=\angle FAP+\angle FPA=\angle FPA+\angle FPC\riff\angle FAP=\angle FPC$，有$\triangle PMC\sim\triangle AGP\riff\dfrac{CM}{PG}=\dfrac{PC}{PA}=\dfrac{\sqrt3}2\riff PG=CD$，再$C,E,H,B,G$五点共圆……