|
|
茂名 杨老师(4747*****) 2014-5-20 15:56:58
求证，对于任意正整数 n ，
[n/1] + [n/2] + [n/3] + … + [n/n] + [√n]
总是偶数。这里， [x] 表示不超过 x 的最大整数。
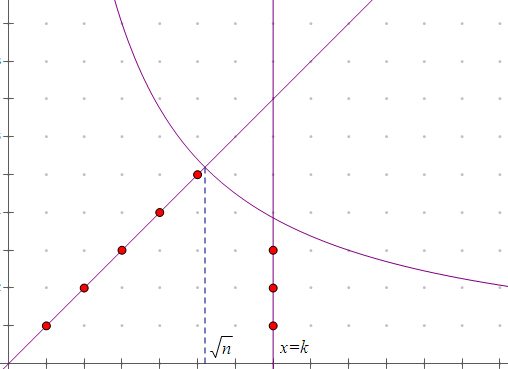
如图，记函数 $y=n/x$ 的图象为曲线 $C$，因为 $[n/k]$ 等于直线 $x=k$ 上且在 $C$ 下方（及 $C$ 上）的整点个数，又由于当 $x>n$ 时 $[n/x]=0$，可见 $[n/1] + [n/2] + [n/3] +\cdots+ [n/n]$ 等于 $C$ 下方（含 $C$）的所有整点的个数。
因为直线 $y=x$ 与 $C$ 交于 $\bigl(\sqrt n,\sqrt n\bigr)$，可见 $\bigl[\sqrt n\bigr]$ 等于直线 $y=x$ 上且在 $C$ 下方（及 $C$ 上）的整点个数。
因此，若用以上所述的格点个数来表示 $[n/1] + [n/2] + [n/3] +\cdots+ [n/n]+\bigl[\sqrt n\bigr]$，那么直线 $y=x$ 上的格点被计算了两次，而不在 $y=x$ 上的则由于图形关于 $y=x$ 对称，必然成对出现，所以 $[n/1] + [n/2] + [n/3] +\cdots+ [n/n]+\bigl[\sqrt n\bigr]$ 必然为偶数。 |
|
isee
Posted 2014-5-20 20:27
