|
|
广雅杨(5257*****) 2014-05-19 23:03:08
此题怎么做？
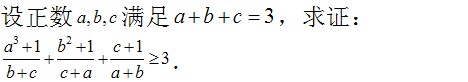
广州kuing/kun 23:20:42
我可以说这个不等式不成立么……
广州kuing/kun 23:23:17
a = 7/8, b = 9/8, c = 1 验证下……
广雅杨(5257*****) 2014-05-20 20:58:06
此题怎么做？
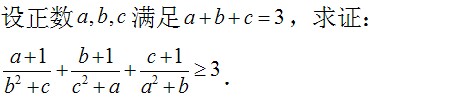
由条件及柯西不等式，有
\begin{align*}
\sum\frac{a+1}{b^2+c}&=\sum\frac{(2a+c)^2(a+1)^2}{(2a+c)^2(a+1)(b^2+c)} \\
& \geqslant \frac{\left( \sum(2a+c)(a+1) \right)^2}{\sum(2a+c)^2(a+1)(b^2+c)} \\
& =\frac{9\left( 2\sum a^2+\sum ca+3\sum a \right)^2}{\sum(2a+c)^2(3a+3)(3b^2+3c)} \\
& =\frac{3\left( \sum a \right)\left( 2\sum a^2+\sum ab+\left( \sum a \right)^2 \right)^2}{\sum(2a+c)^2(4a+b+c)(3b^2+ac+bc+c^2)},
\end{align*}
故此要证原不等式只需证
\[\left( \sum a \right)\left( 2\sum a^2+\sum ab+\left( \sum a \right)^2 \right)^2\geqslant \sum(2a+c)^2(4a+b+c)(3b^2+ac+bc+c^2),\]
为方便书写，记 $p=a+b+c$, $q=ab+bc+ca$，则上式展开整理等价于
\[9(p^2-4q)(a^2b+b^2c+c^2a+abc)+9(11p^2-5q)abc+8p^3(p^2-4q)+pq(p^2-3q)\geqslant 0, \quad (*)\]
若 $p^2\geqslant 4q$，式 (*) 显然成立，而当 $p^2<4q$ 时，由均值知 $p^2\geqslant 3q$，即 $4q>p^2\geqslant 3q$，此时，由已知的经典不等式
\[a^2b+b^2c+c^2a+abc\leqslant \frac4{27}p^3\]以及 Schur 不等式\[abc\geqslant \frac{4pq-p^3}9,\]
可知要证式 (*) 只需证
\[9(p^2-4q)\cdot \frac4{27}p^3+9(11p^2-5q)\cdot \frac{4pq-p^3}9+8p^3(p^2-4q)+pq(p^2-3q)\geqslant 0,\]
因式分解等价于
\[\frac13p(23q-5p^2)(p^2-3q)\geqslant 0,\]
由 $4q>p^2\geqslant 3q$ 可知显然成立。
综上，原不等式获证。 |
|
睡仙
Posted 2014-5-23 16:13
