请教几个几何题，谢谢

fangfang

kuing

第一题可以参考这个链接 forum.php?mod=viewthread&tid=2500

fangfang

原来这么难啊，难怪不会做！谢谢kuing

kuing

这些求角度题都是看似容易实则很难……我基本上都不会
其余的两题得等isee来看了……

战巡

回复 1# fangfang


如图，作$AE=AC$，且$E$在$CD$延长线上
易证$∠ADB=∠ADE=76\du$，$AE=AB$，又显然两个三角形都是锐角的（因为另一个对应的三角形是$△ACD$，显然为钝角）
可证$△ADB≌△ADE$，有$∠DBA=∠DEA=60\du=∠DCA$
因此$A, B, C, D$共圆，$∠CDB=∠CAB=28\du, ∠DBC=∠DAC=44\du-28\du=16\du$

战巡

回复 1# fangfang



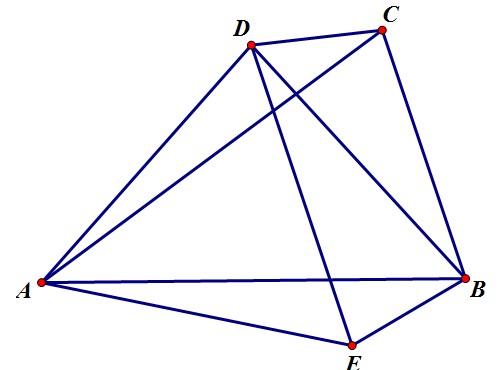
作正三角形$△AED$，其他连线如图
易证$AD=BD, ∠ABC=∠ACB=72\du, AB=AC$，又易知$∠BDE=∠ADB-∠ADE=84\du-60\du=24\du$
$AD=DE=BD$，可知$A, E, B$都在$D$为圆心$AD$为半径的圆上，有$∠BAE=\frac{1}{2}∠BDE=12\du=∠DAC$
那么$AD=AE, AB=AC, ∠DAC=∠BAE$，有$△ADC≌△ABE, ∠DCA=∠ABE=\frac{1}{2}∠ADE=30\du$

tommywong

sin50sin20sin(110-x)sin40=sin60sin50sinxsin30
sin20sin(110-x)sin40=sin60sinxsin30
sin20sin40sin110=(sin30sin60+sin20sin40cos110)tanx
x=30

sin(60-2x)sinxsin(92-2x)sin76=sin60sin(x+60)sin28sin(2x-16)
x=16

sin36sin24sinxsin84=sin48sin72sin(84-x)sin12
sinxsin84sin78=sin48sin54sin(84-x)
(sin84sin78+sin48sin54cos84)tanx=sin48sin54sin84
x=30