|
|
爱好者-郭郭(3631*****) 23:19:06
看下这个题
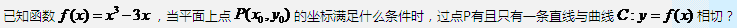
下面考虑稍一般的三次函数 $f(x)=ax^3+cx$($a\ne0$)的情形。
设切点为 $(t,at^3+ct)$,则易得此切点处的切线为 $y-at^3-ct=(3at^2+c)(x-t)$,因 $(x_0,y_0)$ 在切线上,所以 $y_0-at^3-ct=(3at^2+c)(x_0-t)$,整理得
\[2 a t^3 - 3 a t^2 x_0 - c x_0 + y_0 = 0,\]
那么,过 $(x_0,y_0)$ 的切线有且只有一条当且仅当满足上式的 $t$ 有且只有一个。
记 $g(t)=2 a t^3 - 3 a t^2 x_0 - c x_0 + y_0$,则 $g'(t)=6at(t-x_0)$。
(1)若 $x_0=0$,则 $g(t)$ 为单调函数,满足要求;
(2)若 $x_0\ne0$,则 $g(t)$ 有两个极值点 $g(0)$ 和 $g(x_0)$,所以 $g(t)$ 有且只有一个零点当且仅当 $g(0)g(x_0)>0$,即
\[(- c x_0 + y_0)(- a x_0^3 -c x_0 + y_0)>0,\]
也即
\[\bigl(y_0-f'(0)x_0\bigr)\bigl(y_0-f(x_0)\bigr)>0.\]
综合(1)(2)知,过 $(x_0,y_0)$ 的切线有且只有一条当且仅当 $x_0=0$ 或 $\bigl(y_0-f'(0)x_0\bigr)\bigl(y_0-f(x_0)\bigr)>0$,易知这也等价于
\[(x_0,y_0) \in \{(0,0)\}\cup\bigl\{(x,y)\mid \bigl(y-f'(0)x\bigr)\bigl(y-f(x)\bigr)>0\bigr\}.\]
结果的几何意义很明显,而对于更一般的三次函数,只需将上述结论作平移即得。
还可以进一步得出两切线、三切线的条件,懒得写了,估计也是老掉牙的东西…… |
|