再看2014年天津理科数学19题（文科数学20题）

踏歌而来

已知 $q$ 和 $n$ 均为给定的大于 1 的自然数．设集合 $M=\{0,1,2, \cdots, q-1\}$ ，集合 $A=\{x \mid x=x_1+\sqrt{x_2 q}+\cdots+x_n q^{n-1}, x_i \in M, i = 1,2, \dots,n\}$
（I）当 $q=2, n=3$ 时，用列举法表示集合 $A$ ；
（II）设 $s, t \in A, s=a_1+a_2 q+\cdots+a_n q^{n-1}, t=b_1+b_2 q+\cdots+b_n q^{n-1}$ ，其中 $a_i, b_t \in M$ ， $i=1,2, \cdots, n$ ．证明：若 $a_n<b_n$ ，则 $s<t$ ．
（Ⅱ）的标准答案如下图。

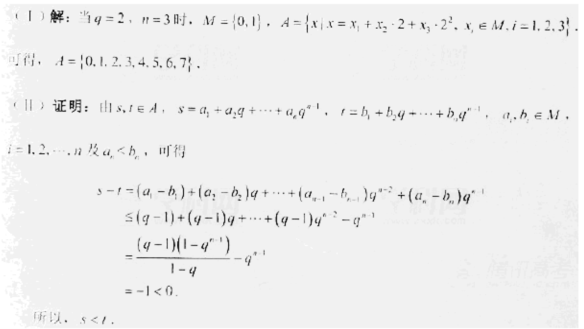
$不太好理解，因为a_1、a_2、…、a_n都小于等于q-1，但在题目中又分为两段，a_{n-1}-b_{n-1}≤q-1，a_n-b_n≤-1。$

还有一种 解析版： http://wenku.baidu.com/link?url=SCEsuRMSLr7HDo7SbvMiiiGxA2KhOGW1riF-sCPp_eZQB3qTicprNDB5NVX1bQIxv3rWlNxdZM3ctMZMQbZ8L98RmhQecHUlSWZcQfuWj_W

截取的图形如下：

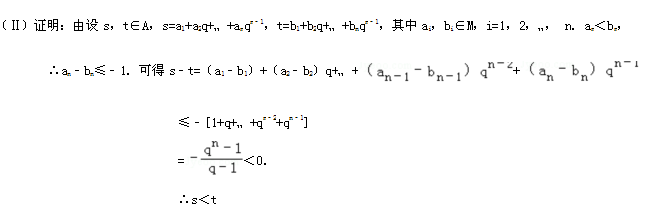
$这道题目做得不对，误以为a_n<b_n对于所有自然数都成立，但题目的本来意思是n取大于等于2的自然数。$

可以简单地证明。
$因为a_2<b_2,a_3<b_3,……，a_n<b_n，所以有a_2-b_2≤-1，a_3-b_3≤-1，…，a_n-b_n≤-1$
$又a1-b1≤q-1，所以s-t≤(q-1)-q-q^2……-q^{n-1}=-1-q^2-……-q^{n-1}<0$
所以命题得证。

kuing

我的贴子就写过
forum.php?mod=redirect&goto=findpost& … id=2803&pid=9930（5楼）

踏歌而来

回复 2# kuing

不错，你做得挺好！

kuing

我还想说的是，其实题目的意思是最后一个 an<bn ，前面的都没这关系，你的理解也不对。官方标答正确。

踏歌而来

标答不好理解。
$a_n<b_n$，n是大于1 的数，包括$a_2<b_2$吧？题目的意思应该不是专指最后一项。
标准答案给我们的启示是，即使$a_n<b_n$专指最后一项也成立。

kuing

回复 5# 踏歌而来

题意本来就是专指最后一项，不包括 a2<b2。你的理解不行。

踏歌而来

好，我们再听听别人的吧。

kuing

回复 7# 踏歌而来

怎么？还觉得你的正确吗？

请再看清楚题目：已知 q 和 n 均为给定的大于 1 的自然数。
请问是否理解什么叫“给定的”？

其实题目在表达上得已经很注意了，特意写上“给定的”就是为了避免产生你这种误解，可惜你还是当作没看见。

tommywong

这理解一点也不重要

kuing

回复 9# tommywong

题意理解错，就会有1楼那样的误证，不重要？

踏歌而来

回复 10# kuing

你的理解是对的。“给定的”与“不给定”是有所区别。
标答是推荐答案。

hbghlyj

踏歌而来 发表于 2014-8-8 03:42
（Ⅱ）的标准答案如下图。

$不太好理解，因为a_1、a_2、…、a_n都小于等于q-1，但在题目中又分为两段，a ...

图片失效了！