来自某教师群的平几证垂直

kuing

掲阳石(7368*****) 15:47:50

请帮忙解决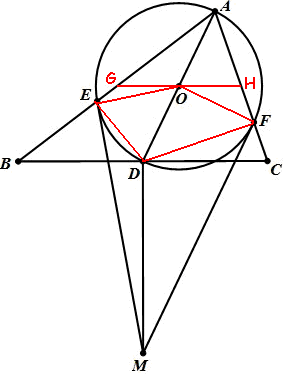

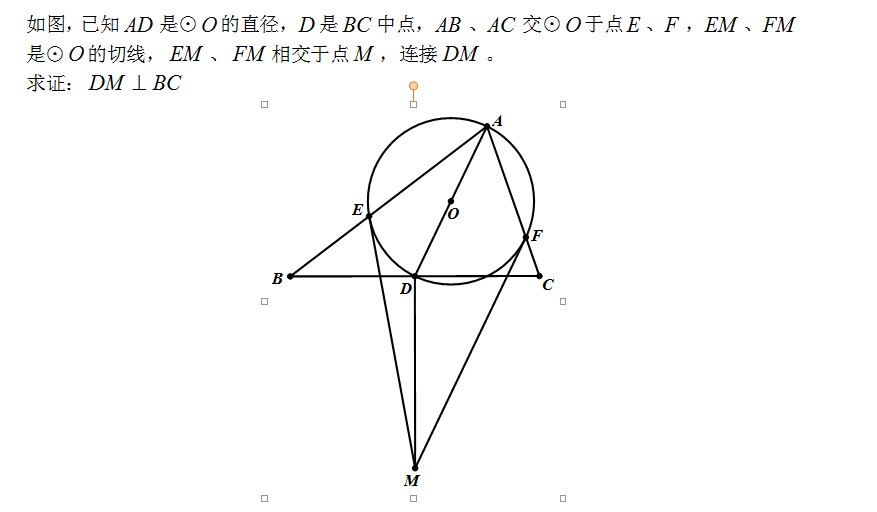
如图，过 $O$ 作 $DM$ 的垂线分别与 $AB$, $AC$ 交于 $G$, $H$，连结 $OE$, $OF$, $DE$, $DF$，下面证明 $OG=OH$。

由于 $OG\perp MD$ 且 $OE\perp ME$，可得 $\angle GOE=\angle DME$，又 $\angle DEM=\angle DAE=\angle GEO$，所以 $\triangle GEO\sim \triangle DEM$，且其相似比为 $EO:EM$。

同理，有 $\triangle HFO\sim \triangle DFM$，且其相似比为 $FO:FM$，显然 $EO:EM=FO:FM$，即这两对相似三角形的相似比相同，故由公共边 $DM$ 即得 $OG=OH$。

由 $OG=OH$ 及 $DB=DC$ 可得 $GH\px BC$，即 $DM\perp BC$。

乌贼

在数学吧看到的另一解法（99楼）
  tieba.baidu.com/p/1046035106?pn=4

isee

回复 2# 乌贼


    这是一道经典题，典型的竞赛题，随便翻了竞赛书，应该有很多不同的解法。我印象里，M大在人教论坛也解过。