证明：四边形中形成的三角形外接圆过定点

isee

给定凸四边形$ABCD$，$BC=AD$，且$BC$与$AD$不平行。设点$E$和点$F$分别在边$BC$与边$AD$上，满足$BE=DF$。
直线$AC$和$BD$相交于点$P$，直线$BD$和$EF$相交于点$Q$，直线$AC$和$EF$相交于点$R$。
证明：当点$E$和$F$变动时，$\triangle PQR$的外接圆经过除点$P$外的另一个定点。

乌贼

尼玛，这种题就像躲猫猫，我藏你找……
幸亏有几何画板，点是找到了（外接圆与$EF$平分线的下交点），证明不会{:curse:}

乌贼

复杂
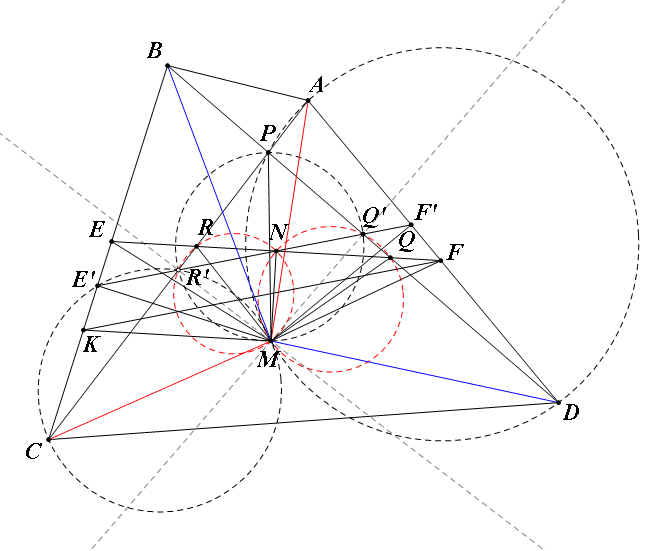
分别作$AC,BD$的垂直平分线交于点$M,M$就是所求的定点。证明如下：
延长$AC,BD$的中点$R',Q'$交$BC,AD$于$E',F'$，连接$MA,MB,MC,MD,\triangle BMC\cong\triangle MDA\riff\angle MAD=\angle MCB,\angle BMC=\angle DMA\riff\angle AMC=\angle BMD\riff\angle MAC=\angle MDB\riff A,P,M,D$四点共圆$\riff\angle MAD=\angle MPD$又$P,R',Q',M$四点共圆$\riff\angle MPD=\angle MR'Q'=\angle MCB\riff M,C,E',R'$四点共圆$\riff ME'\perp BC$同理$MF'\perp AD$
有$\triangle BE'M\cong\triangle DF'M\riff ME'=MF'\riff\angle ME'F'=\angle MF'E'\riff\angle BE'F'=\angle AF'E'$。
分别在$BC,AD$上取点$E,F$使$BE=DF\riff EE'=FF'$，连接$EF$分别交$AC,E'F',BD$于$R,N,Q$，过$F$作$FK//F'E'$交$BC$于$K$，则四边形$E'F'FK$为等腰梯形，有$EE'=E'K=F'F\riff N$为$EF$中点，$MN$是等腰$\triangle MEF$的高，故
$M,R',R,N$四点共圆，$M,Q,Q',N$四点共圆$\riff\angle R'MR=\angle R'NR=\angle Q'NQ=\angle Q'MQ\riff\angle RMQ=\angle R'MQ'=\angle APD\\\riff P,Q,R,M$四点共圆

isee

厉害。

乌贼

回复 3# 乌贼
这样简单点：作$AC,BD$垂直平分线交点$M$，连接$MA,MB,MC,MD,ME,MF$
$\triangle BMC\cong\triangle DMA\riff\angle BMC=\angle DMA\riff\angle BMD=\angle AMC\riff\angle ACM=\angle FEM=\angle4$
$\triangle MBE\cong\triangle MDFriff ME=MF,\angle BME=\angle DMF=\angle2\riff\angle EMF=\angle BMD\riff\angle MEF=\angle MBD=\angle4$
由图$C,E,R,M$四点共圆，$A,B,E,M$四点共圆有$\angle3=\angle1+\angle2$故
$P,R,M,Q$四点共圆。

其妙

厉害。
isee 发表于 2014-9-20 08:50

同意

kuing

那画面太美我不敢看…………

其妙

那画面太美我不敢看…………
kuing 发表于 2014-9-20 15:13

你怎么知道我也不敢看？

乌贼

原来是人教论坛初中版上的题，是中考模拟题
bbs.pep.com.cn/forum.php?mod=viewthread&t … d=2721147&extra=

isee

回复 9# 乌贼

原帖估计是层进的，即使是中考模拟，也是附加题之类的了。

这题的背景是密克点。绝对的竞赛内容。

乌贼

回复 10# isee
那人教上这样断章取义不是坑死人了