转人教论坛几何题

乌贼

bbs.pep.com.cn/forum.php?mod=viewthread&t … 415&extra=page=1

乌贼

第一题：取$BE$中点$K$，连接$FK$，作$\triangle FBK$外接圆，过$K$作直线$KP//EF$分别交$BC,BD,BA$和圆于$N,M,P$。有四边形$PFCK$为矩形。$\angle PBC=90^\circ\riff PB//AN\riff\angle OBP=\angle OAN$，又$AO=BO\riff\triangle OBP\cong\triangle OAN\riff$四边形$APBN$为矩形，有$AP=NB\riff\triangle AFP\cong\triangle NMB\riff AF=NM=\dfrac12CD$

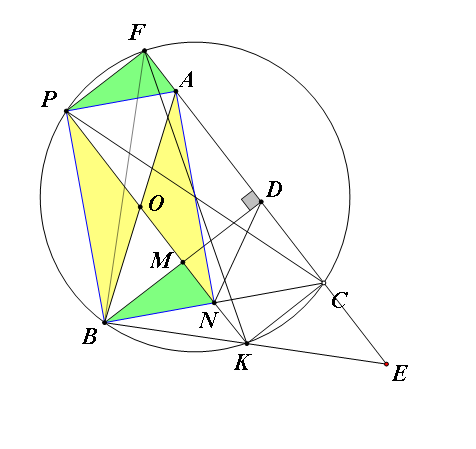
期待简洁证法。

乌贼

人教论坛不让链接过来了{:curse:}

kuing

回复 3# 乌贼

去掉 http 应该可以贴过去，像这样 kuing.orzweb.net/viewthread.php?tid=3062

isee

第一题：取$BE$中点$K$，连接$FK$，作$\triangle FBK$外接圆，过$K$作直线$KP//EF$分别交$BC,BD,BA$和圆于$ ...
乌贼 发表于 2014-10-1 04:26

另解。

第一感觉，直接算——

在三角形ABD中，直接勾股定理\[a^2+(x+a)(2y)=(a+y)^2,\]直接展开就是需要证明的结论。

乌贼

回复 5# isee
第三题如何证明：
  $\triangle ABC$中，$E$为$BC$上任意点，$\angle DEB=\angle FEC$，$I、H、G$分别为$AE、DF、BC$中点，若$I、H、G$共线，求证$AB=AC$。

isee

回复  isee
第三题如何证明：
  $\triangle ABC$中，$E$为$BC$上任意点，$\angle DEB=\angle FEC$，$I、H ...
乌贼 发表于 2014-10-2 14:36

未深入思考原题，不过，先看原题更强的命题（名题，牛顿线）：


如图，证三中点 G，H，I 共线：

乌贼

回复 7# isee
感觉是变式

其妙

明·吴承恩《西游记》第34回：“他两个在半空中，这场好杀。棋逢对手，将遇良才。”

乌贼

回复 4# kuing
这样是可以了