来自人教群之几何题

乌贼

锐角$\triangle ABC$中，$BD$是$AC$边上的高，$E$是$AB$上的一点，满足$\angle AEC=45^\circ,BD=2CE$，且$DE//BC$。求证：$CE=AD+AC$。

郝酒

梅内 (AB:BE)(EF:FC)(CD:DA)=1
平行 AB:BE=AC:CD
所以 AD:AC=EF:FC
合比 AD:(AD+AC)=EF:(EF+FC)
发现需证 AD=EF（或AC=CF）

这个跟BC没什么关系了（当然要知道FD=2EF，AF平分ED）
过F作FG垂直EF，过A作AH垂直EC。FG//AH
考虑到ADHF四点共圆，所以……（后面突然想不明白了，窘）

乌贼

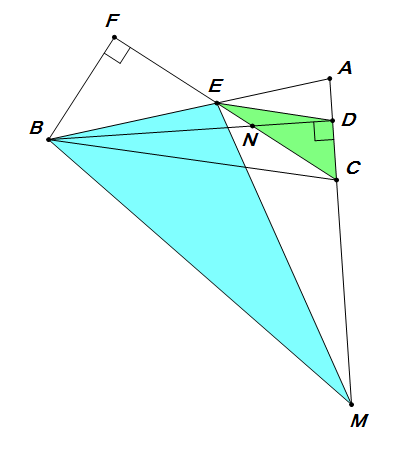
延长$ DC $至$ M $，使$ BD=DM $，作等腰直角$ \triangle BFE,\angle BFE=90\du  $，$ N $为$ BD $与$ CE $交点。有$ BECM $四点共圆，又$ DE\px BC $，所以\[ \angle ECD=\angle MBE\\\angle CED=\angle ECB=\angle BME \]得\[ \triangle EDC\sim \triangle MEB\riff \dfrac{\sqrt{2}BF}{CD}=\dfrac{BE}{CD}=\dfrac{BM}{CE}=\dfrac{\sqrt{2}BD}{CE}=2\sqrt{2}\riff BF=2CD \]由\[ \triangle BFN\sim \triangle CDN\riff BN=2CN,FN=2DN \\\triangle EDN\sim \angle CBN\riff EN=\dfrac{1}{2}DN=\dfrac{1}{4}FN=\dfrac{1}{3}FE\]直角$ \triangle BFN $中\[ BN=5EN\riff CD=\dfrac{3}{2}EN,BD=7EN\\\riff BC=\dfrac{\sqrt{205}}{2}EN\riff DE=\dfrac{\sqrt{205}}{5}EN\\\riff\dfrac{AD}{CD}=\dfrac{DE}{BC-DE}=\dfrac{2}{3}\riff AD=EN\\\riff CE=\dfrac{7}{2}EN=AD+AC\]