问两个和旋转有关的几何题

abababa

$P$是正方形$ABCD$内一点，$PA+PB+PC$的最小值是$\sqrt{2}+\sqrt{6}$，求正方形边长

$\odot O_1,\odot O_2$是同心圆，半径分别为$r_1, r_2$，且$r_1<r_2$正$\triangle ABC$内接于$\odot O_1$，点$P$是$\odot O_2$上的点，求证$PA,PB,PC$能构成三角形，求这个三角形的面积

第二题的能构成三角形旋转一下就行了，面积怎么求呢？

爪机专用

第一个就是费马点吧

abababa

是的，第一个就是费马点，经楼上这么一提醒想起来了，已经解决了。
第二个在一位网友的提示下也解决了

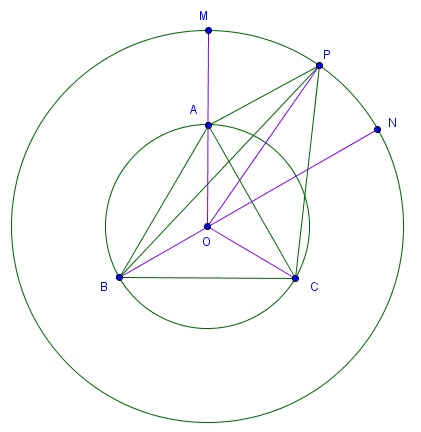
根据对称性，只要考虑$P$在弧$MN$上的情况就行了
因为$\angle POB = \angle AOB+\angle POM > \angle AOC-\angle POM = \angle POC$，所以$PB > PC$
因为$\angle POA = \angle NOA-\angle PON < \angle NOC+\angle PON = \angle POC$，所以$PA < PC$
这样就有$PB > PC > PA$
然后设坐标$A(0,2), B(-\sqrt{3},-1), C(\sqrt{3},-1), P(c, s)$
其中$c = \frac{2r_2}{r_1}\cos\theta, s = \frac{2r_2}{r_1}\sin\theta$，于是$c^2+s^2 = \frac{4r_2^2}{r_1^2}$
$PA^2 = (c-0)^2+(s-2)^2, PB^2 = (c+\sqrt{3})^2+(s+1)^2, PC^2 = (c-\sqrt{3})^2+(s+1)^2$
然后用秦九韶公式就有$4S'^2 = PA^2 \cdot PB^2-(\frac{PA^2+PB^2-PC^2}{2})^2 = \frac{3}{4}(c^2+s^2-4)^2 = \frac{12(r_2^2-r_1^2)^2}{r_1^4}$
算出$S' = \sqrt{3}\frac{r_2^2-r_1^2}{r_1^2}$，然后因为$\frac{S}{S'} = (\frac{r_1}{2})^2$，所以$S = \frac{\sqrt{3}}{4}(r_2^2-r_1^2)$

青青子衿

第一道题是  2008年广东省中考题
haokan.baidu.com/v?pd=wisenatural&vid=16165979334471797579

abababa

回复 4# 青青子衿

谢谢。现在对平面几何题兴趣不像开始那么大了，不过想看一些初高中里，带一些高等背景内容的题。