来自人教群的 $\abs x+\abs y=\sqrt{(x-1)^2+(y-1)^2}$

kuing

渝爱好者-学习(3308*****)  15:13:54

题目：已知实数 $x$, $y$ 满足 $\abs x+\abs y=\sqrt{(x-1)^2+(y-1)^2}$，求 $x^2+y^2$ 的最小值。

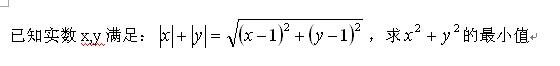
解：将条件等式两边平方得
\[x^2+y^2+2\abs{xy}=(x-1)^2+(y-1)^2,\]
化简得
\[\abs{xy}=1-x-y\geqslant 1-\abs x-\abs y,\]
故
\[2\leqslant (\abs x+1)(\abs y+1)\leqslant \frac{(\abs x+\abs y+2)^2}4,\]
得到
\[\abs x+\abs y\geqslant 2\sqrt2-2,\]
所以
\[x^2+y^2\geqslant \frac{(\abs x+\abs y)^2}2\geqslant \frac{\bigl(2\sqrt2-2\bigr)^2}2=6-4\sqrt2,\]
当 $x=y=\sqrt2-1$ 时取等。

羊1234

$\abs{xy}=1-x-y\geqslant 1-\abs x-\abs y$
这个难想到

kuing

回复 2# 小芳

不想分类讨论，想全部都变成绝对值来搞，于是自然就放缩了

yhg1970

也可用数形结合解决。