|
|
kuing
Post time 2014-12-22 15:44
由（1）知 $M$ 正好是左准线与 $x$ 轴的交点，作出左准线，过 $A$, $B$ 分别作左准线的垂线，垂足分别为 $A'$, $B'$，连结 $FA$, $MC$，如图所示。
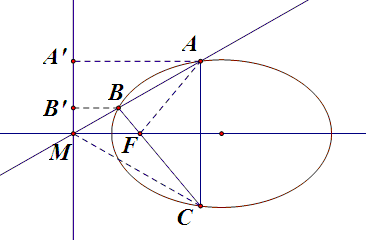
由椭圆第二定义知
\[\frac{FA}{FB}=\frac{AA'}{BB'}=\frac{MA}{MB},\]
可知 $FM$ 是 $\triangle FAB$ 的外角平分线，由此可见 $FA$ 与 $FB$ 的斜率相反，所以 $AC$ 必然与 $x$ 轴垂直，再由 $\angle MAC=60\du$ 即得 $\triangle MAC$ 为等边三角形，所以 $MA$ 的斜率为 $\tan30\du$。 |
|
