|
|
话说昨天人教群里有这么一段
蒙A爱好者云云(9802*****) 18:29:15
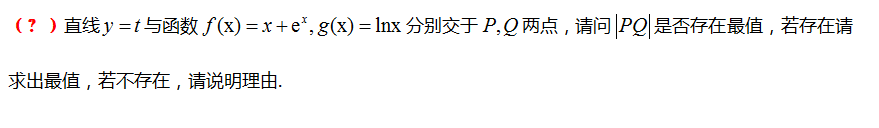
谁做出来给奖金50000元
当时就决定不鸟他了,不过刚才还是忍不住又看了下,想验证一下直觉,看看是不是会出现超越方程。
设 $P$, $Q$ 两点的横坐标分别为 $x_1$, $x_2$,则
\[t=x_1+e^{x_1}=\ln x_2,\]
显然 $x_2=e^t>t>x_1$,故
\[PQ=x_2-x_1,\]
对 $t$ 求导得
\begin{align*}
\frac{\rmd PQ}{\rmd t}&=\frac{\rmd x_2}{\rmd t}-\frac{\rmd x_1}{\rmd t} \\
& =e^t-\frac1{\rmd t/\rmd x_1} \\
& =e^t-\frac1{f'(x_1)} \\
& =e^{x_1+e^{x_1}}-\frac1{1+e^{x_1}},
\end{align*}
那么 $PQ$ 取最值时必然有
\[e^{x_1+e^{x_1}}(1+e^{x_1})=1,\]
换个元可以变简洁些,令 $x_1=\ln u$,代入上式即
\[e^uu(1+u)=1,\]
如无意外地超越方程粗现了,这极可能没有初等解,反正我观察不出特殊解,如果你找到了,那就可以推倒我的直觉。
设上式的唯一正数解为 $u_0$,此时 $t=\ln u_0+u_0$,故 $PQ$ 的最小值就是 $u_0e^{u_0}-\ln u_0$,即 $1/(1+u_0)-\ln u_0$。
题目看来是废了,不过先别急着扔掉,既然方法已经有了,可以试着变废为宝,也就是改变题中的函数,使得最后的方程存在特殊解,当然函数最好不要是直线,不然太简单。
简单点的话试下搞成根号吧,我将 $g(x)$ 稍改下,就改编出如下题目:
改编题:直线 $y=t$($t\geqslant 0$)与函数 $f(x)=x+e^x$, $g(x)=2\sqrt x$ 分别交于 $P$, $Q$ 两点,求 $PQ$ 的最小值。
解:设 $P$, $Q$ 两点的横坐标分别为 $x_1$, $x_2$,则
\[t=x_1+e^{x_1}=2\sqrt{x_2},\]
假设 $x_1\leqslant -1$,则 $e^{x_1}<1$,那么 $x_1+e^{x_1}<0$,与 $t\geqslant0$ 矛盾,所以必有 $x_1>-1$。
下面证明 $x_2>x_1$,如果 $x_1\leqslant0$,则显然成立,而当 $x_1>0$ 时,由于
\[x_2=\frac{t^2}4=\frac{(x_1+e^{x_1})^2}4\geqslant \frac{(2x_1+1)^2}4>x_1,\]
所以 $x_2>x_1$,因此
\[PQ=x_2-x_1,\]
对 $t$ 求导得
\begin{align*}
\frac{\rmd PQ}{\rmd t}&=\frac{\rmd x_2}{\rmd t}-\frac{\rmd x_1}{\rmd t} \\
& =\frac t2-\frac1{\rmd t/\rmd x_1} \\
& =\frac t2-\frac1{f'(x_1)} \\
& =\frac{x_1+e^{x_1}}2-\frac1{1+e^{x_1}} \\
& =\frac{e^{2x_1}+(1+x_1)e^{x_1}+x_1-2}{2(1+e^{x_1})},
\end{align*}
记 $h(x_1)=e^{2x_1}+(1+x_1)e^{x_1}+x_1-2$,由 $x_1>-1$ 易见 $h(x_1)$ 关于 $x_1$ 递增,而显然 $h(0)=0$,可见 $PQ$ 取最小值当且仅当 $x_1=0$,此时 $t=1$, $x_2=1/4$,所以 $PQ$ 的最小值为 $1/4$。 |
|