来自人教群的$x+y-\sqrt{x^2+y^2}$有最大值求参数范围

kuing

豫U教师张琦(3289*****) 2015-3-26 9:10:14

，求简单解法，我的解法太复杂。
附上我的复杂解法：

kuing

其实这显然有几何意义，于是不难得到如下解法。



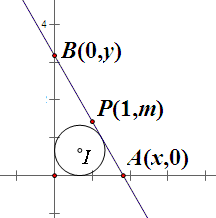
设直线 $l$ 与 $x$, $y$ 轴的正半轴交于 $A(x,0)$, $B(0,y)$，则由 $1/x+m/y=1$ 可知该直线过定点 $P(1,m)$，设 $\triangle OAB$ 的内切圆 $I$ 的半径为 $r$，则表达式 $x+y-\sqrt{x^2+y^2}=2r$。

当直线 $l$ 变动时，内切圆的大小在变化，不难看出，$r$ 存在最大值当且仅当存在某一刻使 $l$ 与内切圆相切于点 $P$。

设切于点 $P$ 时圆心坐标为 $(a,a)$，显然 $P$ 的两坐标均大于 $a$，即 $1>a>0$ 且 $m>a>0$，由 $(1-a)^2+(m-a)^2=a^2$，配方得 $(1+m-a)^2=2m$，故 $a=1+m-\sqrt{2m}$，所以 $1>1+m-\sqrt{2m}>0$ 且 $m>1+m-\sqrt{2m}>0$，解得 $1/2<m<2$。

反之，当 $1/2<m<2$ 时，令 $a=1+m-\sqrt{2m}$，则 $1>a>0$ 且 $m>a>0$，以 $(a,a)$ 为圆心作与 $x$, $y$ 轴相切的圆，则此圆过 $P$，过 $P$ 作圆的切线，则切线必与 $x$, $y$ 轴的正半轴相交。

综上所述，$m$ 的取值范围为 $(1/2,2)$。

kuing

上面的“反之”那段看似多余，但为了严格起见，还是要写上，才能说明是充要的。

kuing

一般地，设点 $P(m,n)$ 在第一象限，则过 $P$ 且与 $x$, $y$ 轴相切的较小圆在 $P$ 处的切线斜率为负当且仅当 $m/n\in(1/2,2)$。
这个命题其实从几何角度也很容易解释，如图，点在粗线上就行，所以 $m/n\in(1/2,2)$，这么看来，其实上面的解法也可以改进，完全不用计算。

kuing

改进后的过程：

引理：设点 $P(m,n)$ 在第一象限，则过 $P$ 且与 $x$, $y$ 轴相切的较小圆在 $P$ 处的切线斜率为负当且仅当 $m/n\in(1/2,2)$。

设直线 $l$ 与 $x$, $y$ 轴的正半轴交于 $A(x,0)$, $B(0,y)$，则由 $1/x+m/y=1$ 可知该直线过定点 $P(1,m)$，设 $\triangle OAB$ 的内切圆 $I$ 的半径为 $r$，如上图，则 $x+y-\sqrt{x^2+y^2}=2r$。

当直线 $l$ 变动时，内切圆的大小在变化，不难看出，$r$ 存在最大值当且仅当存在某一刻使 $l$ 与内切圆相切于点 $P$，这等价于过 $P$ 且与 $x$, $y$ 轴相切的较小圆在 $P$ 处的切线斜率为负，于是由引理即得 $m$ 的取值范围为 $(1/2,2)$。

hjfmhh

不难看出，r  存在最大值当且仅当存在某一刻使 l  与内切圆相切于点 P 。

这句话怎么理解，kuing

hjfmhh

用三角换元也可以

kuing

回复 6# hjfmhh

想象一下，或者用软件画个图动一下

kuing

回复 6# hjfmhh

其实我本来也想说清楚点，不过我的表达能力有限，所以当时就直接带过，靠大家想象了。
这里试着尽力表达下，大概就是内切圆变大时，斜边在绕，如果圆碰到P时斜边没问题，就定了，达到最大值了。如果还没碰到P时斜边就要翘起来了，那内切圆就只能不断接近斜边与轴平行时的大小而达不到最大值。

其妙

回复 9# kuing
有些东西是只可意会不好言传滴