转自人教论坛的两圆连心线上点对两圆切线长之和最大

kuing

原贴链接：bbs.pep.com.cn/forum.php?mod=viewthread&tid=3116625
原贴发贴人：0.1
题目：

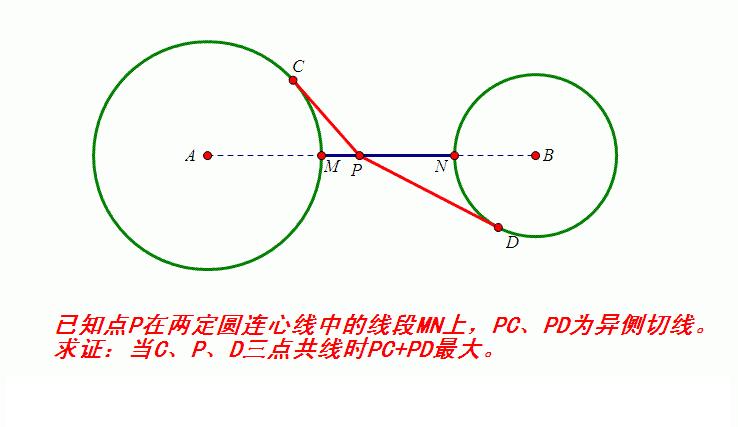
结论真漂亮，贴中我给出了代数证法：
不妨设圆 $A$, $B$ 半径分别为 $R$, $r$，设 $PM=x$, $PN=y$，则由柯西不等式有
\begin{align*}
PC+PD &= \sqrt{(R+x)^2-R^2}+\sqrt{(r+y)^2-r^2} \\
&= \sqrt{x(x+2R)}+\sqrt{y(y+2r)} \\
&\leqslant \sqrt{(x+y)(x+2R+y+2r)} \\
&= \sqrt{MN(MN+2R+2r)},
\end{align*}
等号成立当且仅当 $(x+2R)/x = (y+2r)/y$，即 $x : y = R : r$，易证此时就是三点共线时。

期待漂亮的几何证法

乌贼

转
  bbs.pep.com.cn/forum.php?mod=viewthread&t … 625&extra=page=1
三楼

isee

像是反演变换得到的命题。

kuing

回复 2# 乌贼

牛比

kuing

突然发现人教论坛居然也搞禁止外链图片了，唉……