记录某教师群的一道小不等式

kuing

【师长】广州-程汉波(2872*****) 18:42:49


【军长】广州kuing/kun(2495*****) 18:47:26


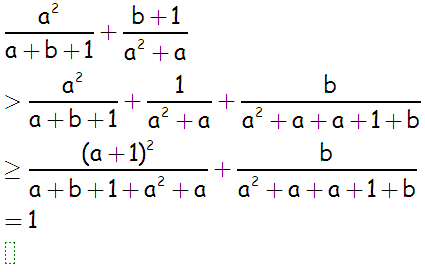
【营长】广州陈泽桐(5956*****) 18:57:00

代码存档：

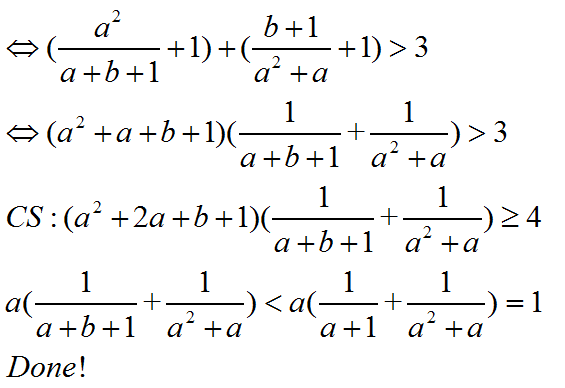
证法一

\begin{align*}

\frac{a^2}{a+b+1}+\frac{b+1}{a^2+a}

&=\frac{a^2+a}{a+b+1}+\frac{a+b+1}{a^2+a}-\frac a{a+b+1}-\frac a{a^2+a} \\

&\geqslant 2-\frac a{a+b+1}-\frac1{a+1} \\

&>2-\frac a{a+b+1}-\frac{1+b}{a+b+1} \\

&=1.

\end{align*}



证法二

\begin{align*}

\frac{a^2}{a+b+1}+\frac{b+1}{a^2+a}

&>\frac{a^2}{a+b+1}+\frac1{a^2+a}+\frac b{a^2+a+a+1+b} \\

&\geqslant \frac{(a+1)^2}{a+b+1+a^2+a}+\frac b{a^2+a+a+1+b} \\

&=1.

\end{align*}



证法三

\begin{align*}

&\iff \frac{a^2}{a+b+1}+1+\frac{b+1}{a^2+a}+1>3 \\

&\iff (a^2+a+b+1)\left( \frac1{a+b+1}+\frac1{a^2+a} \right)>3,

\end{align*}

CS

\begin{gather*}

(a^2+2a+b+1)\left( \frac1{a+b+1}+\frac1{a^2+a} \right)\geqslant 4,\\

a\left( \frac1{a+b+1}+\frac1{a^2+a} \right)<a\left( \frac1{a+1}+\frac1{a^2+a} \right)=1,

\end{gather*}

Done!

其妙

这儿也有多种的解答：
blog.sina.com.cn/s/blog_54df069f0102vgjb.html

其妙

这里还有两道类似的：
1、blog.sina.com.cn/s/blog_54df069f0102vgjb.html
2、

其妙

这是什么群呀？kk变成军长了！

kuing

果然引来了方法党

PS、新浪图片不能直接外链过来，请另存再上传。

其妙

回复 5# kuing
三楼已经重新上传，本楼也有：如下第二题如何解决？

kuing

回复 6# 其妙

被解决了没？

我的证法比较麻烦，如果还没被解决我就写写

其妙

回复 7# kuing
题2没解决，题1见：blog.sina.com.cn/s/blog_54df069f0102vgjb.html

kuing

回复 8# 其妙

那我就写写题2吧。
PS、链接里也没看到题1？

kuing

还有，这些非对称不等式谁出的？

kuing

%证得比较麻烦，希望没错
%期待更好的证法
\(\newcommand\piand{\partial}\)

题目：已知 $a\geqslant 1$, $b>0$，求证
\[\frac1{a+1}+\frac{b^2}{a+b}+\frac a{b^2+b}\geqslant \frac32.\]

证明：我们分三类讨论。

（1）当 $b\geqslant a\geqslant 1$ 时，记
\[f(a,b)=\frac1{a+1}+\frac{b^2}{a+b}+\frac a{b^2+b},\]
对 $a$ 求导得
\begin{align*}
\frac{\piand f(a,b)}{\piand a}
& =-\frac1{(a+1)^2}-\frac{b^2}{(a+b)^2}+\frac1{b^2+b} \\
& \leqslant -\frac1{(b+1)^2}-\frac{b^2}{(b+b)^2}+\frac1{b^2+b} \\
& =\frac{(1-b)(b^2+3b+4)}{4b(b+1)^2} \\
& \leqslant 0,
\end{align*}
即关于 $a$ 递减，所以
\[f(a,b)\geqslant f(b,b)=\frac1{b+1}+\frac{b^2}{b+b}+\frac b{b^2+b}=\frac2{b+1}+\frac{b+1}2-\frac12\geqslant \frac32;\]

（2）当 $a\geqslant b\geqslant 1$ 时，由于序列 $\{b^2,a\}$ 与 $\{1/(a+b),1/(b^2+b)\}$ 显然必为同序，故由排序不等式有
\[\frac1{a+1}+\frac{b^2}{a+b}+\frac a{b^2+b}\geqslant \frac1{a+1}+\frac a{a+b}+\frac{b^2}{b^2+b}=\frac a{a+b}+\frac b{b+1}+\frac1{1+a},\]
注意到有恒等式
\[\frac{a-b}{a+b}+\frac{b-c}{b+c}+\frac{c-a}{c+a}
=\frac{(a-b)(a-c)(b-c)}{(a+b)(a+c)(b+c)},\]
由此可见当 $a\geqslant b\geqslant c$ 时有
\[\sum \frac a{a+b}\geqslant \frac12\sum \frac a{a+b}+\frac12\sum \frac b{a+b}=\frac32,\]
令 $c=1$ 即得需要证的不等式；

（3）当 $a\geqslant 1\geqslant b>0$ 时，由柯西不等式有
\begin{align*}
\frac1{a+1}+\frac{b^2}{a+b}+\frac a{b^2+b}-\frac32
& \geqslant \frac{(1+b)^2}{2a+b+1}+\frac a{b^2+b}-\frac32 \\
& =\frac{(1+b)^2}{2a+b+1}-1+\frac a{b^2+b}-\frac12 \\
& =\frac{b^2+b-2a}{2a+b+1}+\frac{2a-b^2-b}{2(b^2+b)} \\
& =\frac{(2a-b^2-b)(2a+1-2b^2-b)}{2(2a+b+1)(b^2+b)} \\
& \geqslant 0.
\end{align*}

综上所述，原不等式得证。

其妙

回复 11# kuing