来自某教师群的 $1/(k\cdot2^k)$ 求和

kuing

【师长】江门王老师(6538*****) 2015-04-21 8:52:56

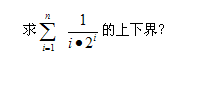
请各位老师帮忙看看

【师长】江门王老师(6538*****) 2015-04-21 9:00:33
上下确界
少写了一个字，不好意思

【师长】江门王老师(6538*****) 2015-04-21 9:06:48
我没有见过试卷原题，学生用纸抄过来的，由于水平有限，所以请教各位老师

话说学生抄来问的题通常都不太想看，往往坑，不过刚才挂机传片闲着看了下，似乎没想象中困难。

下确界就不用说了，上确界就是求
\[\sum_{k=1}^{\infty}\frac1{k\cdot2^k}.\]

令
\[f(x)=\sum_{k=1}^{\infty}\frac{x^{-k}}k,\quad x>1,\]
由于
\[\frac{x^{-k}}k=\int_x^{+\infty}u^{-k-1}\rmd u,\]
于是
\begin{align*}
f(x)&=\int_x^{+\infty}\sum_{k=1}^{\infty}u^{-k-1}\rmd u \\
& =\int_x^{+\infty}\frac{u^{-2}}{1-u^{-1}}\rmd u \\
& =\int_x^{+\infty}\frac1{u-1}-\frac1u\rmd u \\
& =\left. \left( \ln \frac{u-1}u \right) \right|_x^{+\infty} \\
& =\ln \frac x{x-1},
\end{align*}
所以
\[\sum_{k=1}^{\infty}\frac1{k\cdot2^k}=f(2)=\ln 2.\]

希望没什么大问题。

战巡

回复 1# kuing


\[\ln(1+x)=\sum_{k=1}^{\infty}(-1)^{k-1}\frac{x^k}{k}\]
\[\ln(1-\frac{1}{2})=-\ln(2)=-\sum_{k=1}^{\infty}\frac{1}{k·2^k}\]

kuing

回复 2# 战巡

soga 原来泰勒就这么简单，我不熟所以没想到，结果从正面着手就变成1#的解法，不过看上去用到的东西基本些