|
|
 乌贼
乌贼
posted 2015-5-12 13:55
Last edited by 乌贼 2015-5-12 18:48回复 2# kuing
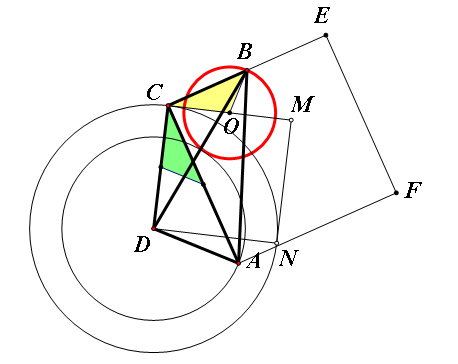
等价于:定线段$DC=\sqrt{5}$,圆$D$,半径$AD=3$,$A$为圆上动点,以$AC$为边长向外作正方形$ACEF$,$CE$中点即是$B$点。
如图,以$DC$为边长作正方形$DCMN$,取$CM,AC,DC$中点$O,P,Q$,有\[ \triangle CBO\cong \triangle CPQ \]有\[ OB=PQ=\dfrac12AD=\dfrac{\sqrt5}{2} \]有$B$点的轨迹是以$O$为圆心,$\dfrac{\sqrt5}{2}$为半径的圆,故……
|
|