来自某教师群的$(\sqrt2+1)^{21}$展开式系数与27约

kuing

【营长】东莞－权哥(2744****)  17:42:47
问大家一个问题：

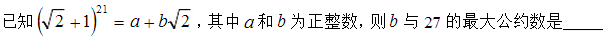
这题除了用二项式定理解决之外，还有什么方法？

记 $\bigl(\sqrt2+1\bigr)^n=a_n+b_n\sqrt2$，其中 $a_n$, $b_n$ 为正整数，则 $a_1=b_1=1$，且
\[a_{n+1}+b_{n+1}\sqrt2=\bigl(\sqrt2+1\bigr)\bigl(a_n+b_n\sqrt2\bigr)
=a_n+2b_n+(a_n+b_n)\sqrt2,\]
所以
\begin{align*}
a_{n+1}&=a_n+2b_n, \\
b_{n+1}&=a_n+b_n,
\end{align*}
消 $a_n$ 有
\[b_{n+2}-b_{n+1}=b_{n+1}-b_n+2b_n,\]
即
\[b_{n+2}=2b_{n+1}+b_n,\]
进而
\[b_{n+2}=2(2b_n+b_{n-1})+b_n
=5b_n+2b_{n-1}
=5(2b_{n-1}+b_{n-2})+2b_{n-1}
=12b_{n-1}+5b_{n-2},\]
由此可见，如果 $3\nmid b_k$，则 $3\nmid b_{k+4}$，故由 $3\nmid b_1$ 即得 $3\nmid b_{4k+1}$，所以 $3\nmid b_{21}$，即 $b$ 与 $27$ 互素。