|
|
ＭεmοΓㄚ 18:03:24
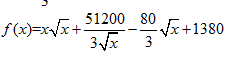
这个怎么用基本不等式求最值？ 
令 $\sqrt x=t$, $51200/3=p$, $80/3=q$，只要求
\[t^3+\frac pt-qt\]
的最小值。待定 $(0,1)$ 内的系数 $x$，有
\begin{align*}
& t^3+\frac pt-qt \\
={}& xt^3+\frac p{3t}+\frac p{3t}+\frac p{3t} +(1-x)t^3+\sqrt{\frac{q^3}{27(1-x)}}+\sqrt{\frac{q^3}{27(1-x)}}-qt -2\sqrt{\frac{q^3}{27(1-x)}} \\
\geqslant{}& 4\sqrt[4]{xt^3\cdot \left( \frac p{3t} \right)^3} +3\sqrt[3]{(1-x)t^3\cdot \frac{q^3}{27(1-x)}}-qt -2\sqrt{\frac{q^3}{27(1-x)}} \\
={}& 4\sqrt[4]{\frac{xp^3}{3^3}}-2\sqrt{\frac{q^3}{27(1-x)}},
\end{align*}
取等条件为
\[
\led
xt^3&=\frac p{3t}, \\
(1-x)t^3&=\sqrt{\frac{q^3}{27(1-x)}},
\endled
\]
消 $t$ 后化简得
\[3(1-x)^2p=xq^2,\]
把 $p$, $q$ 的数值代进去，解得
\[x=\frac89,\]
再代回去化简，即得
\[t^3+\frac pt-qt\geqslant \frac{3200}3\sqrt5,\]
所以 $f(x)$ 的最小值就是
\[\frac{3200}3\sqrt5+1380.\] |
|
爪机专用
posted 2015-5-16 20:35
