|
|
original poster
hongxian
posted 2015-5-29 20:57
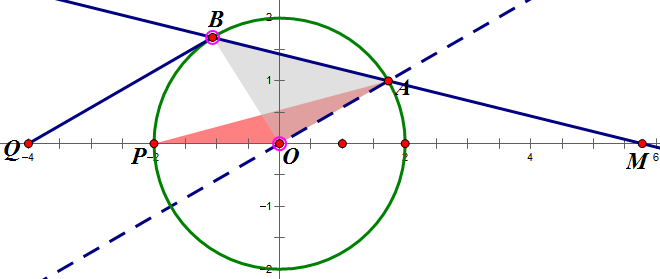
Last edited by hongxian 2015-5-29 21:03变圆一:
变圆$\dfrac{x^2}{4}+\dfrac{y^2}{4}=1$,$Q(4,0)$,$M(m,0)$,$BQ\px OA\Longrightarrow\triangle MOA\sim\triangle MQB\Longrightarrow\dfrac{QB}{OA}=\dfrac{QM}{OM}\Longrightarrow QB=\dfrac{2(4-m)}{m}\in(2,6)\Longrightarrow m\in(1,2)$
变圆二:
变圆$\dfrac{x^2}{4}+\dfrac{y^2}{4}=1$,$Q(-4,0)$,$M(m,0)$,$BQ\px OA\Longrightarrow\triangle MOA\sim\triangle MQB\Longrightarrow\dfrac{QB}{OA}=\dfrac{QM}{OM}\Longrightarrow QB=\dfrac{2(4+m)}{m}\in(2,6)\Longrightarrow m\in(2,+\infty )$

|
|