来自人教群的二次型最值（擦，还玩……

kuing

浙B教师慈溪(6319*****)  16:59:15

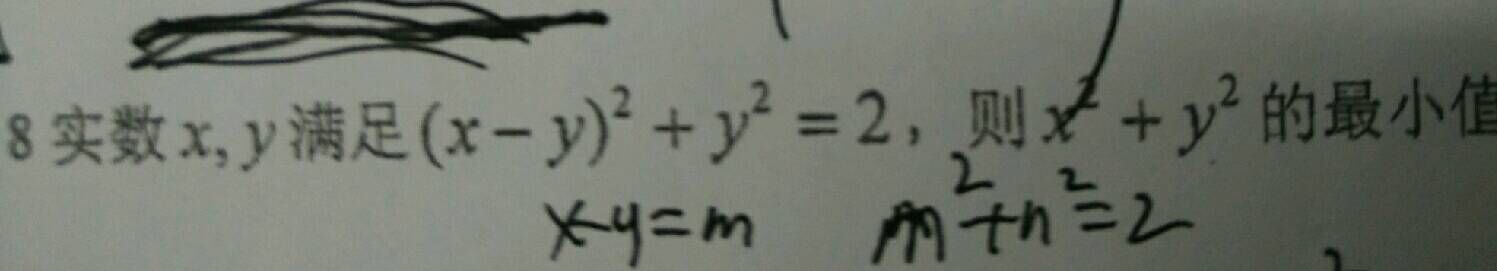
这个题目，不用三角函数换元可以做吗

粤A爱好者kuing(249533164)  17:08:05


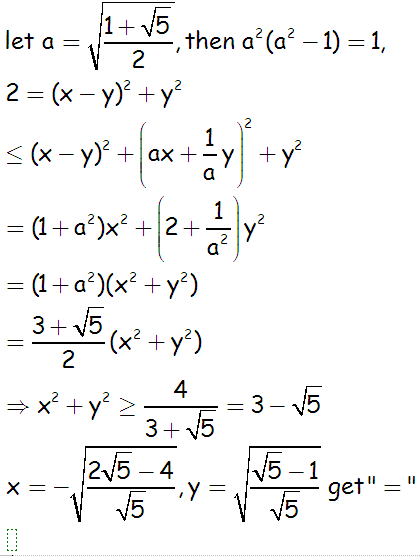
浙B教师慈溪(6319*****)  17:10:40
厉害
很厉害的方法
答案是对的
浙B爱好者T35(3705*****)  17:12:01

浙B教师慈溪(6319*****)  17:12:04
这用了什么方法
浙B爱好者T35(3705*****)  17:12:05
kuing大神

粤A爱好者kuing(249533164)  17:12:18
我也不知道算是什么方法，临时想的
处理二次型最值的方法太多，我也没归纳过

浙B爱好者T35(3705*****)  17:13:06
那你就归纳一下
别这么懒

粤A爱好者kuing(2495*****)  17:13:42
肯定早就被归到烂了，何必重复别人的工作

浙B教师慈溪(6319*****)  17:14:25
你这方法很新鲜，一般人看不懂啊
我是不是解题能力太差了
只会三角函数代换

粤Y爱好者Joseph(1785***)  17:16:03
三角代换有什么不好啊？那是通用方法

粤A爱好者kuing(249533164)  17:16:07
就是加个东西消去 xy 啊，至于加什么还要待定一下系数
最开始那个 a 就是待定解出来的

浙B教师慈溪(6319*****)  17:16:30
哦，明白了

代码存档

令

$$a=\sqrt{\frac{1+\sqrt2}2},$$

则 $a^2(a^2-1)=1$，于是

\begin{align*}

2&=(x-y)^2+y^2 \\ 

 & \leqslant (x-y)^2+\left( ax+\frac1ay \right)^2+y^2 \\ 

 & =(1+a^2)x^2+\left( 2+\frac1{a^2} \right)y^2 \\ 

 & =(1+a^2)(x^2+y^2) \\ 

 & =\frac{3+\sqrt5}2(x^2+y^2),

\end{align*}

即得

$$x^2+y^2\geqslant \frac4{3+\sqrt5}=3-\sqrt5,$$

取等条件为

$$x=\pm\sqrt{\frac{2\sqrt5-4}{\sqrt5}},y=\mp\sqrt{\frac{\sqrt5-1}{\sqrt5}}.$$

kuing

还真是又玩，想起这贴 forum.php?mod=viewthread&tid=2737 我在求椭圆长短轴的时候其实也是在玩道题。
而且上面的方法和链接中的待定系数均值其实本质上也是差不多的东西。

其妙