来自人教群的似曾相识的三元轮换不等式

kuing

鲁Q爱好者昵称(7868*****)  19:19:13

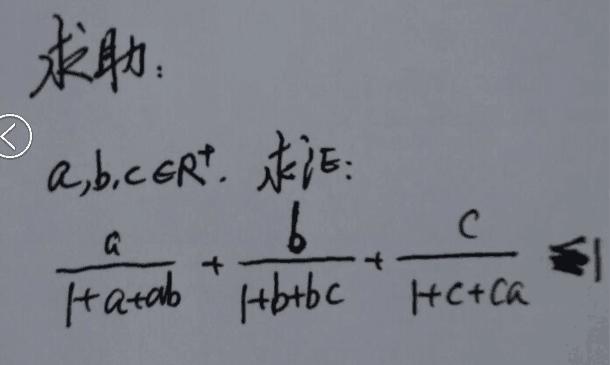
@粤A爱好者kuing✈  有何简法

以前好像见过，也可能只是类似，没想出什么简法。
鉴于当 abc=1 时是恒等式，所以就由这里入手，求导玩。

设 $abc=m$，则
\begin{align*}
& \frac{a}{1+a+ab}+\frac{b}{1+b+bc}+\frac{c}{1+c+ca} \\
={}& \frac{ca}{c+ca+m}+\frac{m}{ca+m+mc}+\frac{c}{1+c+ca} \\
={}& \frac{ca}{c+ca+m}+\frac{1}{1+c}\left( 1-\frac{ca}{ca+m+mc} \right)+\frac{c}{1+c+ca} \\
={}& f(m),
\end{align*}
求导即得
\[f'(m)=-\frac{ca}{(c+ca+m)^2}+\frac{ca}{(ca+m+mc)^2},\]
可见当 $0<m<1$ 时 $f'(m)>0$，当 $m>1$ 时 $f'(m)<0$，故 $f(m)\leqslant f(1)=1$。

你们也来玩玩。

kuing

注：其实直接对任意一个变量求导来做都是差不多的，我整个m出来是为了更加一目了然 些。

hjfmhh

当 abc=1 时是恒等式,这个是通分化简吗？还是有简单方法

爪机专用

回复 3# hjfmhh

第二行的m变成1就知道了

hjfmhh

回复 4# 爪机专用
    $ac/(c+a+1)+ab/(a+ab+1)+bc/(b+bc+1)$
    $=a/(1+a+ab)+b/(1+b+bc)+c/(1+c+ca)$
    $=1/(bc+1+b)+1/(ac+1+c)+1/(ab+1+a)$
是这三个式子相加吧

kuing

当 abc=1 时是恒等式,这个是通分化简吗？还是有简单方法
hjfmhh 发表于 2015-6-19 21:45

\begin{align*}
& \frac{a}{1+a+ab}+\frac{b}{1+b+bc}+\frac{c}{1+c+ca} \\  
={}& \frac{ca}{c+ca+\color{red}m}+\frac{\color{red}m}{ca+\color{red}m+\color{red}mc}+\frac{c}{1+c+ca}
\end{align*}
这几个m是1的话还不显然=1吗？

hjfmhh

嗯，谢谢kuing