不建系能解吗？

guanmo1

有解答是建系解决的，不建系能解吗？

kuing

用几何意义呗，如图，$N$ 为 $AC$ 中点，$D$, $E$ 关于 $N$ 对称，$NF\px AM$ 且 $FH\perp AM$ 于 $H$。

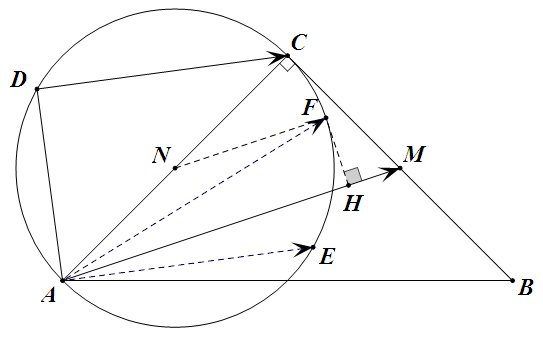
$\vv{DC}\cdot\vv{AM}=\vv{AE}\cdot\vv{AM}$，由数量积的几何意义知，当 $E$ 到达 $F$ 时取最大值为 $AH\cdot AM$。
易见 $AM=2\sqrt5$, $AH=NF+AN\cos\angle CAM=2+4/\sqrt5$，故最大值为 $4\sqrt5+8$。

tommywong

$t=\angle DCA$
$\vec{DC}=(|\vec{AC}|\cos^2{t})\dfrac{\vec{AC}}{|\vec{AC}|}+(|\vec{AC}|\sin{t}\cos{t})\dfrac{\vec{CB}}{|\vec{CB}|}=\cos^2{t}\vec{AC}-\sin{t}\cos{t}\vec{BC}$
$\vec{AM}=\dfrac{1}{2}\vec{AC}+\dfrac{1}{2}\vec{AB}=\vec{AC}+\dfrac{1}{2}\vec{BC}$
$\vec{AC}\cdot\vec{BC}=0$
$\vec{DC}\cdot\vec{AM}=16\cos^2{t}-8\sin{t}\cos{t}$

guanmo1

回复 2# kuing


    赞一个，想到几何意义了，但没深入下去。

guanmo1

回复 3# tommywong


    漂亮！

活着＆存在