最值问题

hjfmhh

第一题是不是最值不存在：（x,0)到两定点(0,-1),(12,-4)距离差的最大值，但感觉最大值取不到

kuing

嗯，1没最大值，应该改为求最小值，要么就改改数据。

kuing

2就配方成 $\sqrt{(x^2 - 2)^2 + (x + 3)^2}-\sqrt{(x^2-1)^2+x^2}$

kuing

3就配方成 $\sqrt{(x - 5)^2 + (y + 12)^2}+\sqrt{(x + 5)^2 + (y + 12)^2}$

kuing

4易知 $\sqrt{10x-x^2-21}$, $\sqrt{7x-x^2-10}$ 的图象都为半圆，把它们分别画出来，设直线 $x=x_0$ 与两者相交，作出交点处的切线，如图所示。



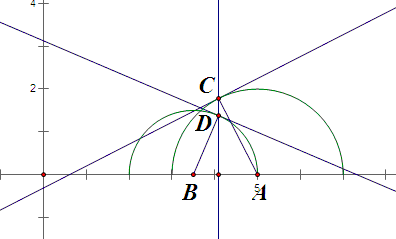
则 $f(x)$ 取最大值当且仅当两切线斜率互反，亦即 $\angle DBA=\angle CAB=\theta$ 时。

此时显然 $BD\cos\theta+AC\cos\theta=AB$，代入数据解得 $\cos\theta=3/7$，所以 $x_0=5-2\cos\theta=29/7$，所以 $f(x)$ 的最大值就是 $f(29/7)$。

至于最小值，显然只要比较 $f(3)$ 与 $f(5)$ 即可，下略。

其妙

题目4，这里好像有：blog.sina.com.cn/s/blog_54df069f0101dxz0.html

kuing

回复 6# 其妙

有就有，别“好像”好伐

hjfmhh

回复 4# kuing

这个表示圆$x^2+y^2=169$上的点到定点(5,-12),(-5,-12)距离之和最大，接下来还是不会，kuing能麻烦再写一下吗？先谢谢了

kuing

回复 8# hjfmhh

这两个点也在圆上……

hjfmhh

回复 9# kuing


    嗯，这两点在圆上我也看出来了接下来还是没思路

kuing

回复 10# hjfmhh

擦，等腰时最大，常识来的啊……

hjfmhh

回复 11# kuing

我是这样处理的，不知道对否？kuing的常识不知道是什么？是什么定理吗？求指教

kuing

回复 12# hjfmhh

$\triangle ABC$ 中，$BC$ 和 $\angle A$ 都为定值，求 $AB+AC$ 的最大值。这难道不是常识题？用正弦定理和和差化积就行了，余弦定理也行，随便整都行。

hjfmhh

回复 13# kuing


    谢谢kuing

hjfmhh

回复 5# kuing

根据kuing的图的解法，请问kuing怎么知道f(x)最大时，两条切线斜率为什么刚好相反。谢谢

kuing

回复 15# hjfmhh

…………增加率与减少率相等啊

hjfmhh

回复 16# kuing


    可否具体一点，还是不理解，谢谢

kuing

回复 17# hjfmhh

想一下导数的意义啊

hjfmhh

对$f(x)=\sqrt{10x-x^2-21}+\sqrt{7x-x^2-10}$进行求导，导数就是切线斜率，求极值点。是不是就这么理解。不懂您的增加率和减少率

其妙

回复  kuing

这个表示圆$x^2+y^2=169$上的点到定点$(5,-12),(-5,-12)$距离之和最大，接下来还是不会，kuing能麻烦再写一下吗？先谢谢了
hjfmhh 发表于 2015-7-11 18:19

看看这里的题目是否是你需要的：blog.sina.com.cn/s/blog_54df069f0101f23n.html