|
|
浙B爱好者渣渣(3705*****) 21:03:16
就硬算?
浙B爱好者渣渣(3705*****) 21:18:37
我硬算的
把俩圆半径算出来
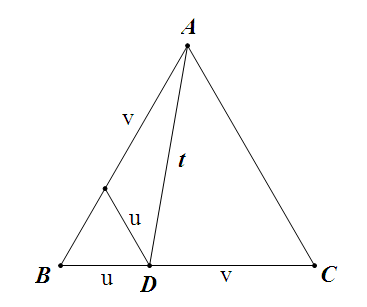
设 $BD=u$, $DC=v$, $AD=t$,由上图可知 $t^2=u^2+v^2+uv$,于是
\[2=\frac{r_C}{r_B}=\frac{\S{ACD}}{\S{ABD}}\cdot \frac{C_{\triangle ABD}}{C_{\triangle ACD}}=\frac vu\cdot \frac{2u+v+\sqrt{u^2+v^2+uv}}{u+2v+\sqrt{u^2+v^2+uv}},\]
解得
\[\frac uv=\frac{1+\sqrt{33}}{16},\]
故
\[\frac{BD}{AB}=\frac u{u+v}=\frac{1+\sqrt{33}}{17+\sqrt{33}}=\frac{-1+\sqrt{33}}{16}.\] |
|