|
|
粤B学生86鱼(1608******) 20:49:15
\begin{align*}
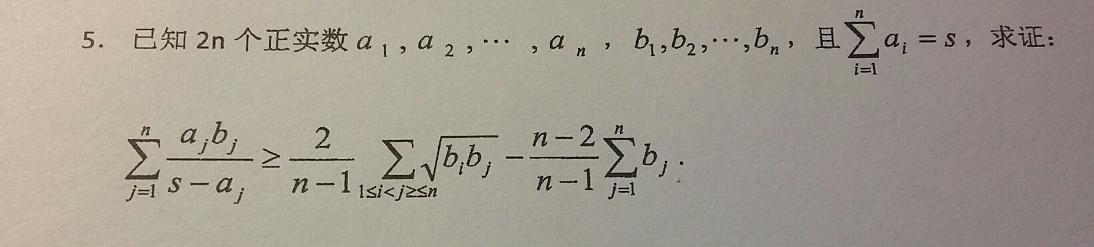
& \sum_{i=1}^n\frac{a_ib_i}{s-a_i}\geqslant \frac2{n-1}\sum_{1\leqslant i<j\leqslant n}\sqrt{b_ib_j}-\frac{n-2}{n-1}\sum_{i=1}^nb_i \\
&\iff (n-1)\sum_{i=1}^n\frac{a_ib_i}{s-a_i}\geqslant 2\sum_{1\leqslant i<j\leqslant n}\sqrt{b_ib_j}-(n-2)\sum_{i=1}^nb_i \\
&\iff (n-1)\sum_{i=1}^n\left( \frac{a_ib_i}{s-a_i}+b_i \right)\geqslant 2\sum_{1\leqslant i<j\leqslant n}\sqrt{b_ib_j}+\sum_{i=1}^nb_i \\
&\iff (n-1)s\sum_{i=1}^n\frac{b_i}{s-a_i}\geqslant \left( \sum_{i=1}^n\sqrt{b_i} \right)^2 \\
&\iff \sum_{i=1}^n(s-a_i)\sum_{i=1}^n\frac{b_i}{s-a_i}\geqslant \left( \sum_{i=1}^n\sqrt{b_i} \right)^2,
\end{align*}
由柯西显然成立。 |
|
