来自某教师群的知中线要面积最大的一般情况

kuing

韶关黄老师(1284******) 9:15:56

各位前辈，这一题，求教。

广州刘<hnli********com> 9:35:40
用海伦公式十基本不等式即可


广州二中邓Sir.(9022***) 9:56:31
这道题其实是有个典故的
如果要给学生做，可以加一个第一问：求动点A的轨迹方程，这样就可以化难为易，得出解决问题的通法了
广州二中－L.M.(5237****) 9:57:38
正解
轨迹为圆
广州二中邓Sir.(9022***) 9:57:56
哈哈，对的
把中点改在三等分点，四等分点，就是这个题目的外延了，题目重新包装一下，就是很好的变式教学案例

广州kuing(249533164) 10:22:59
设两中线交于G，刚S(ABC)=3S(GBC)=3/2*GB*GC*sin∠BGC=54sin∠BGC，所以当BG⊥GC时面积最大，易得此时AB=6√5
两中线长为定值都可以这么做，等腰可以减弱

广州二中邓Sir.(9022***) 10:27:14
恩，好思路
如果原题那个已知条件不是中点，是三等分点呢

广州kuing(249533164) 10:33:17
还是可以的，不过要先证明交点分两线之比为定值，可以用梅氏定理证

闲着没事写个一般情况的过程吧，其实也不是什么新东西了吧。

在 $\triangle ABC$ 中，$E$, $F$ 在 $AC$, $AB$ 上，已知 $AF:FB=\lambda$, $AE:EC=\mu$, $BE=m$, $CF=n$，求 $\S{ABC}$ 的最大值。



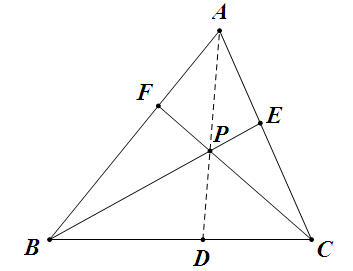
解：如图，设 $BE$, $CF$ 交于 $P$，$AP$ 交 $BC$ 于 $D$，由梅氏定理有
\[\frac{BP}{PE}\cdot \frac{EC}{CA}\cdot \frac{AF}{FB}=1\iff\frac{BP}{PE}\cdot \frac1{1+\mu }\cdot \lambda =1\iff\frac{BP}{PE}=\frac{1+\mu }{\lambda },\]
所以
\[PB=\frac{1+\mu }{1+\lambda +\mu }m,\]
同理
\[PC=\frac{1+\lambda }{1+\lambda +\mu }n,\]
由塞瓦定理有
\[\frac{AF}{FB}\cdot \frac{BD}{DC}\cdot \frac{CE}{EA}=1\iff\lambda \cdot \frac{BD}{DC}\cdot \frac1{\mu }=1\iff\frac{BD}{DC}=\frac{\mu }{\lambda },\]
由梅氏定理有
\[\frac{AP}{PD}\cdot \frac{DB}{BC}\cdot \frac{CE}{EA}=1\iff\frac{AP}{PD}\cdot \frac{\mu }{\lambda +\mu }\cdot \frac1{\mu }=1\iff\frac{AP}{PD}=\lambda +\mu ,\]
从而
\begin{align*}
\S{ABC}&=(1+\lambda +\mu )\S{PBC}, \\
& =\frac12(1+\lambda +\mu )PB\cdot PC\cdot \sin \angle BPC \\
& =\frac{(1+\lambda )(1+\mu )}{2(1+\lambda +\mu )}mn\sin \angle BPC, \\
& \leqslant \frac{(1+\lambda )(1+\mu )}{2(1+\lambda +\mu )}mn,
\end{align*}
当且仅当 $PB\perp PC$ 时取等。

isee

果然是看到这个，还有个印象。。。。。

isee

闲着没事写个一般情况的过程吧，其实也不是什么新东西了吧。

在 $\triangle ABC$ 中，$E$, $F$ 在 $AC$,  ...
kuing 发表于 2016-1-10 17:52

    我今天碰到是求三角形ADB的面积最大值。这实际为阿氏圆了，就简单些了。

    若求三角形ABD的面积最大，则以BD所在的直线为x轴，线段BD中点为原点O，建立直角坐标系，可得点A的轨迹方程为圆，且圆心在x轴上。



    晕，原来聊天里早说了。。。。。。。


。