来自某教师群的 $\sum a/(bc+1)$ 范围

kuing

【军长】广州王勇成老师(5234*****)  14:31:15

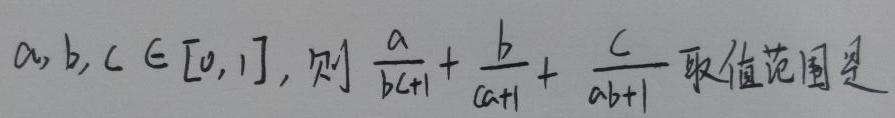
请教大神

显然当 $a=b=c=0$ 时原式取最小值 $0$，另一方面，由于对于任意 $x$, $y\in[0,1]$ 有 $(1-x)(1-y)\geqslant0\iff x+y\leqslant 1+xy$，故此有
\[
\led
b+c&\leqslant 1+bc, \\
a+bc&\leqslant 1+abc
\endled
\riff
a+b+c\leqslant 2+abc,
\]
所以
\[\frac a{bc+1}+\frac b{ca+1}+\frac c{ab+1}\leqslant \frac{a+b+c}{abc+1}\leqslant \frac{2+abc}{abc+1}\leqslant 2,\]
当 $(a,b,c)=(0,1,1)$ 时取等，故此原式的取值范围为 $[0,2]$。


PS、总感觉还有更简洁的证法，晚点再想想，先眯一会……

abababa

能不能用$y=\frac{a^2}{k+a}+\frac{b^2}{k+b}+\frac{c^2}{k+c}$，其中$k=abc\ge 0$，$y$当$k\to 0$时最大，为$y=a+b+c$，当$k\to 0$时$a,b,c$中至少有一个趋向于$0$，不妨设是$c\to 0$，这样$y=a+b$，最大就是$2$。

kuing

果然有更简洁的解法

【军长】广州王勇成老师(5234*****)  16:03:18

kuing

能不能用$y=\frac{a^2}{k+a}+\frac{b^2}{k+b}+\frac{c^2}{k+c}$，其中$k=abc\ge 0$，$y$当$k\to 0$时最大，为$y=a+b+c$，当$k\to 0$时$a,b,c$中至少有一个趋向于$0$，不妨设是$c\to 0$，这样$y=a+b$，最大就是$2$。
abababa 发表于 2016-1-23 15:44

没看懂

游客

我帮你整理一下哈：

kuing

回复 5# 游客

yeah，这样写起来更简洁