来自某教师群的1/ab+1/bc+1/cd+1/da=1不等式(及若干纸老虎)

kuing

广州邓朝发(7316*****)  21:47:37

看着挺吓人，一玩之下发现其实是纸老虎。

条件去分母得 $(a+c)(b+d)=abcd$，所以原不等式等价于
\[\frac{(a+c)^2(b+d)^2}{abcd}+16\geqslant 8\sqrt{(a+c)\left( \frac1a+\frac1c \right)}+8\sqrt{(b+d)\left( \frac1b+\frac1d \right)},\]
整理为
\[2\cdot \frac{(a+c)^2}{4ac}\cdot \frac{(b+d)^2}{4bd}+2\geqslant \sqrt{\frac{(a+c)^2}{ac}}+\sqrt{\frac{(b+d)^2}{bd}},\]
则由均值得
\[
2\cdot \frac{(a+c)^2}{4ac}\cdot \frac{(b+d)^2}{4bd}+2 \geqslant \frac{(a+c)^2}{4ac}+1+\frac{(b+d)^2}{4bd}+1
\geqslant \sqrt{\frac{(a+c)^2}{ac}}+\sqrt{\frac{(b+d)^2}{bd}},
\]
即得证。

kuing

还有一题也是纸老虎，就不另开新帖了。

广州邓朝发(7316*****)  21:44:53

只要别被吓倒，放胆放缩就会发现很简单
\[\sum\sqrt{\frac{y+z}{2x}}\geqslant \sum\frac{\sqrt y+\sqrt z}{2\sqrt x}=\sum\frac{\sqrt x}2\left( \frac1{\sqrt y}+\frac1{\sqrt z} \right)\geqslant \sum\sqrt{\frac x{\sqrt{yz}}}\geqslant \sum\sqrt{\frac{2x}{y+z}}.\]

kuing

这个也有点纸老虎的赶脚：

广州郭子伟(kuing)(249533164) 14:23:22
有木有题？
广州邓朝发(7316*****) 14:24:41
有的，

先看三元的，由 $3=a^2+b^2+c^2\geqslant 3\sqrt[3]{a^2b^2c^2}$ 得 $abc\leqslant1$，故只需证更强式
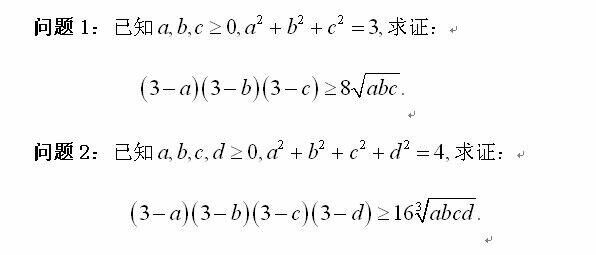
\[(3-a)(3-b)(3-c)\geqslant8,\]
（之所以说是纸老虎就因为右边的根号竟然是可以不要的）
利用切线方法，可以先证明当 $a\in[0,2]$ 时恒有
\[\ln(3-a)\geqslant \frac14(1-a^2)+\ln2,\]
此式求导易证，过程从略，从而
\[\ln(3-a)+\ln(3-b)+\ln(3-c)\geqslant \frac14(3-a^2-b^2-c^2)+3\ln2=\ln8,\]
即得证。

四元的也是，那个三次根式同样可以直接不要，过程完全类似。

kuing

广州邓朝发(7316*****)  22:41:35


这个老虎有点猛@广州郭子伟(kuing)

……

广州郭子伟(kuing)(249533164)  23:05:41
其实也并不猛，纯粹看观察力，观察到就一行解决了：


……

广州邓朝发(7316*****)  23:10:57

代码存档：
\[\sum\frac{(b+c-a)^2}{b^2+2c^2}
=\sum\frac{(b^2+bc-ab)^2}{b^4+2b^2c^2}
\geqslant\frac{\left( \sum(b^2+bc-ab) \right)^2}{\sum(b^4+2b^2c^2)}
=1.\]