来自某教师群的线性规划题

kuing

广州黄开鹏(1649*****) 22:34:36

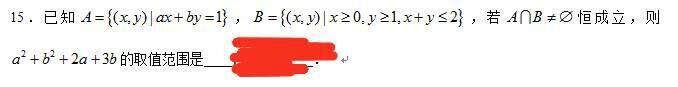
给大家分享一个好题

当时群里已经有人写了分类讨论画图的解法，这里就不贴了。

刚才鼓捣了好一会儿，总算搞出了既不分类也不画图，还能玩不等式的纯代数解法。

首先说明原式无最大值，取 $b=0$，则 $(1/a,1)\in A$，当 $a\geqslant 1$ 时显然也有 $(1/a,1)\in B$，可见当 $b=0$, $a\to+\infty$ 时总存在 $(1/a,1)\in A\cap B$，满足题意，所以原式无最大值。

下面求原式的最小值，依题意，存在 $(m,n)$ 满足 $am+bn=1$, $m\geqslant 0$, $n\geqslant 1$, $m+n\leqslant 2$，配方得
\[a^2+b^2+2a+3b=(a+1)^2+\left( b+\frac32 \right)^2-\frac{13}4,\]
由柯西不等式得
\[(m^2+n^2)\left( (a+1)^2+\left( b+\frac32 \right)^2 \right)\geqslant \left( m(a+1)+n\left( b+\frac32 \right) \right)^2=\frac{(2m+3n+2)^2}4,\]
所以
\[a^2+b^2+2a+3b\geqslant \frac{(2m+3n+2)^2}{4(m^2+n^2)}-\frac{13}4,\]
由 $m\geqslant 0$, $n\geqslant 1$, $m+n\leqslant 2$ 得
\[\frac{(2m+3n+2)^2}{4(m^2+n^2)}\geqslant \frac{(2m+3n+m+n)^2}{4(m^2+n^2)}=4+\frac{m(24n-7m)}{4(m^2+n^2)},\]
而 $24n\geqslant 24>7m$，所以
\[\frac{(2m+3n+2)^2}{4(m^2+n^2)}\geqslant 4,\]
即
\[a^2+b^2+2a+3b\geqslant 4-\frac{13}4=\frac34,\]
当 $m=0$, $n=2$, $a=-1$, $b=1/2$ 时取等，所以原式的最小值就是 $3/4$。

力工

回复 1# kuing

凌晨两点在撸题，真是专家！酷阴请接受楼下的摸白(膜拜)。

游客

角色互换后再作图，比较直观，也是常用手法。
过点(u,u)和点(0,v)作直线L，再求点(-1,-3/2)到直线L的的距离d，最后求d的最小值。
(其中1/2<=u<=1,u<=v<=1)

游客