|
|
【渣^5】川A爱好者zhcosin(5323*****) 12:23:23
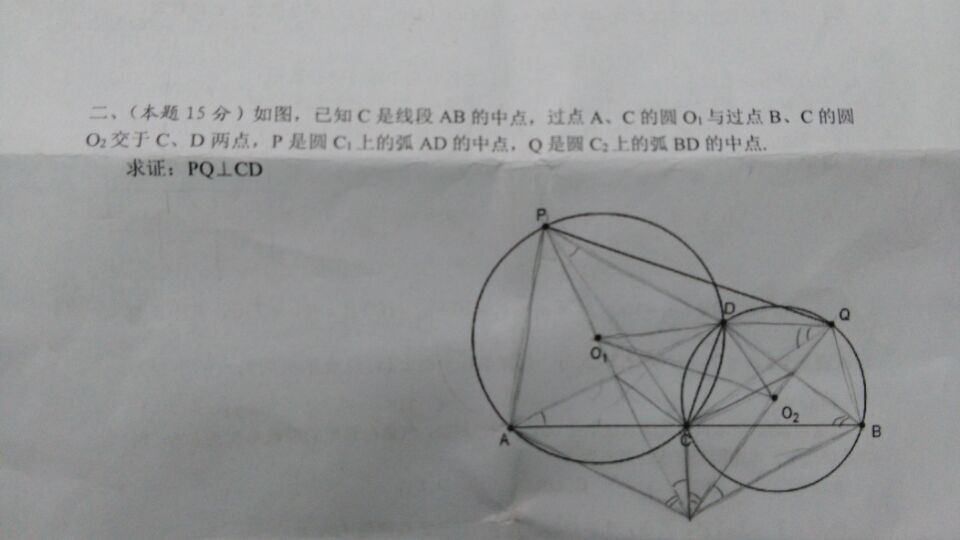
\[CP=\frac{CA+CD}{2\cos\angle PCD}.\]
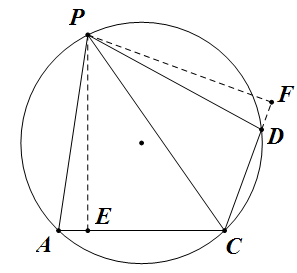
如图，作 $PE\perp CA$, $PF\perp CD$，易证 $\triangle PAE\cong\triangle PDF$，则 $CA+CD=CE+CF=2CF$，所以
\[CP=\frac{CF}{\cos\angle PCD}=\frac{CA+CD}{2\cos\angle PCD}.\]
同理有
\[CQ=\frac{CB+CD}{2\cos\angle QCD},\]
因为 $\angle PCA=\angle PCD$, $\angle QCB=\angle QCD$，所以 $\angle PCQ=90\du$，于是
\[\frac{CP}{CQ}=\frac{\cos\angle QCD}{\cos\angle PCD}=\frac{\sin\angle PCD}{\cos\angle PCD}=\tan\angle PCD,\]
由此即得 $CD\perp PQ$。 |
|
Tesla35
Posted 2016-3-4 20:57
