来自某教师群昨天的一道看似是函数题的不等式

kuing

佛山杜国强(2905*****) 10:29:14

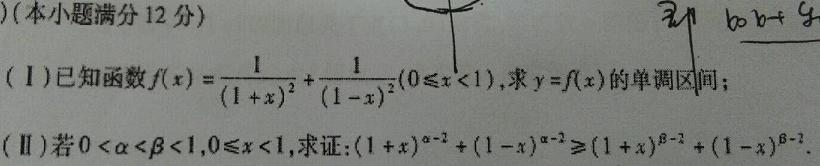
分享个题

（II）为方便打代码，将 $\alpha$, $\beta$ 用 $a$, $b$ 代替，由题设，有 $(1+x)^{a-2}\leqslant (1-x)^{a-2}$ 且 $(1+x)^{b-a}\geqslant (1-x)^{b-a}$，于是由切比雪夫不等式，有
\begin{align*}
(1+x)^{b-2}+(1-x)^{b-2}&=(1+x)^{a-2}(1+x)^{b-a}+(1-x)^{a-2}(1-x)^{b-a} \\
& \leqslant \frac12\bigl( (1+x)^{a-2}+(1-x)^{a-2} \bigr)\bigl( (1+x)^{b-a}+(1-x)^{b-a} \bigr),
\end{align*}
因为 $0<b-a<1$，则由幂平均不等式，有
\[\left( \frac{(1+x)^{b-a}+(1-x)^{b-a}}2 \right)^{1/(b-a)}\leqslant \frac{1+x+1-x}2=1 \riff (1+x)^{b-a}+(1-x)^{b-a}\leqslant 2,\]
所以
\[(1+x)^{b-2}+(1-x)^{b-2}\leqslant (1+x)^{a-2}+(1-x)^{a-2}.\]

hbghlyj

在aops看到一个类似的:

...
But by the power means inequality,
$$(1+d_x)^{m-2}+(1-d_x) ^{m-2}\ge(1+d_x)^{n-2}+(1-d_x) ^{n-2}$$
We are done. The right part later.