一个 三个中点共线 问题

isee

做得很复杂，三楼。

问题，题如图：

isee

做得很复杂。

题如图：
isee 发表于 2016-3-11 21:01

文字如下：

如图，$\triangle ABC \cong \triangle BDE,AB=BD,AC=BE,BC=DE$，$M,N$分别是$AB，BD$的中点，$MN$的延长线交$CE$于点$P$，求证：$P$是$CE$的中点。

isee

取$CE$的中点$P'$，容易证明$P'N\perp GH$且互相平分。

进一步，再证明$\triangle HIM \sim \triangle ADE$(两边成比例为$1:2$，夹角相等)，于是$HM=GM$.

$MN \perp GH$，这表明$P'$就是这$P$点。

kuing

容易证明如下结论：
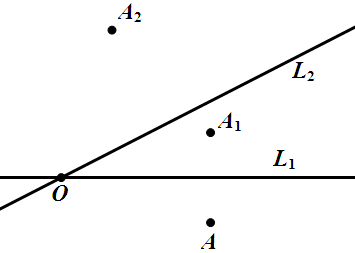
如图，点 $A$ 与 $A_1$ 关于 $L_1$ 对称，将 $A_1$ 绕 $O$ 逆时针旋转 $\theta$ 得到 $A_2$，又将 $L_1$ 绕 $O$ 逆时针旋转 $\theta/2$ 得到 $L_2$，则 $A$ 与 $A_2$ 关于 $L_2$ 对称。

　　　　

回到原题，
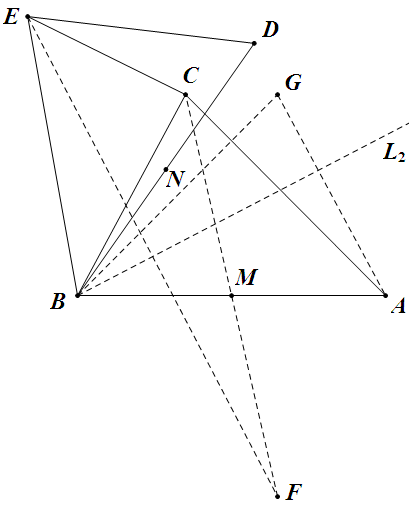
如图，设 $\angle ABD=\theta$，作 $\angle ABD$ 的平分线 $L_2$，倍长 $CM$ 到 $F$，$G$ 与 $F$ 关于 $AB$ 对称，则由全等关系易见 $G$ 绕 $B$ 逆时针旋转 $\theta$ 后就是 $E$，根据上面的结论，$E$, $F$ 关于 $L_2$ 对称，又显然 $M$, $N$ 也关于 $L_2$ 对称，因此 $MN\px EF$，所以 $MN$ 与 $CE$ 的交点必然为中点。

isee

容易证明如下结论：
如图，点 $A$ 与 $A_1$ 关于 $L_1$ 对称，将 $A_1$ 绕 $O$ 逆时针旋转 $\theta$ 得到 $ ...
kuing 发表于 2016-3-11 22:43

这方法不错，直接证法。

不过，倍长CM后，注意$\triangle BFA \cong \triangle BDE$，这样$EF \perp L_2，MN \perp L_2$，引理也不需要了。

kuing

回复 5# isee

O，确实可以。
我想的时候是先想到 G 再弄到 F 去的，然后想起那个引理，就这么搞了粗来，没再反过来思考下……

isee

回复 6# kuing


    明白……

乌贼

回复 5# isee
不能画图。借图说，易证$ ADEF $为等腰梯形，$AD\px EF$
有$EF\px MN$，$M$为$CF$中点，$\triangle ECF$中，$MN$平分$EC$

isee

回复  isee
不能画图。借图说，易证$ ADEF $为等腰梯形，$AD\px EF$
有$EF\px MN$，$M$为$CF$中点，$\tria ...
乌贼 发表于 2016-3-12 22:55

好久不见。

PS：后来，的确得到了初二全等方法，此题。如下图：