|
|
赣B爱好者远远(1530*****) 18:38:22
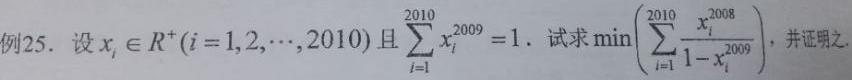
求证明
\[\sum_{i=1}^n \frac{a_i^{(n-2)/(n-1)}}{1-a_i}.\]
由均值,有
\[(n-1)a_i(1-a_i)^{n-1}\leqslant \left( \frac{(n-1)a_i+(n-1)(1-a_i)}n \right)^n=\left( \frac{n-1}n \right)^n,\]
得到
\[a_i^{1/(n-1)}(1-a_i)\leqslant \frac{n-1}{n^{n/(n-1)}},\]
所以
\[\frac{a_i^{(n-2)/(n-1)}}{1-a_i}=\frac{a_i}{a_i^{1/(n-1)}(1-a_i)}\geqslant \frac{n^{n/(n-1)}}{n-1}a_i,\]
求和即得
\[\sum_{i=1}^n \frac{a_i^{(n-2)/(n-1)}}{1-a_i}\geqslant \frac{n^{n/(n-1)}}{n-1},\]
当 $a_1=a_2=\cdots=a_n=1/n$ 时取等号,所以上式右边就是最小值, |
|