来自某教师群的 $\sum\frac1{1+a^4}\ge2$

kuing

广州邓朝发(7316*****) 22:28:25

直接去分母可知原不等式等价于
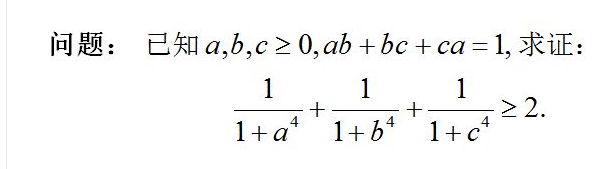
\[a^4b^4+b^4c^4+c^4a^4+2a^4b^4c^4\leqslant 1,\]
由条件得
\[a^2b^2+b^2c^2+c^2a^2\leqslant (ab+bc+ca)^2=1,\]
令 $a^2b^2=x$, $b^2c^2=y$, $c^2a^2=z$，则只需证明当 $x$, $y$, $z\geqslant 0$ 且 $x+y+z\leqslant 1$ 时有
\[x^2+y^2+z^2+2xyz\leqslant 1,\]
上式整理等价于
\[(x+yz)^2\leqslant (1-y^2)(1-z^2),\]
事实上
\[(x+yz)^2\leqslant (1-y-z+yz)^2=(1-y)^2(1-z)^2\leqslant (1-y^2)(1-z^2),\]
即得证。