来自人教论坛的费马点求 $(PA+PC)/PB$

kuing

原帖链接：bbs.pep.com.cn/forum.php?mod=viewthread&tid=3141140
题目：

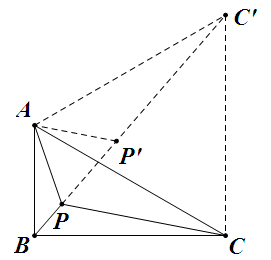
由已知等式可知 $P$ 为费马点，如图，将 $\triangle APC$ 绕 $A$ 旋转 $60\du$ 至 $\triangle AP'C'$，则 $\triangle APP'$, $\triangle ACC'$ 均为等边三角形，故 $B$, $P$, $P'$, $C'$ 共线，所以
\[PA+PB+PC=BP+PP'+P'C'=BC',\]
恰好 $\angle BCC'$ 为直角，故易得 $BC'=\sqrt7$，又恰好 $\angle BAC'=120\du$，故 $\triangle BPA\sim \triangle BAC$，所以
\[BP\cdot BC'=BA^2=1,\]
那么
\[\frac{PA+PC}{PB}=\frac{BC'}{PB}-1=BC'^2-1=6.\]

Tesla35

原贴的图不见了啊。

kuing

回复 2# Tesla35

没办法，要怪就只能怪那边不让传附件……

kuing

原题印象中是用三角函数等式来表达费马点的