来自人教群的一道错题$a+b+c+d=a^2+b^2+c^2+d^2=3$

kuing

赣B爱好者远远(1530*****)  13:15:27

想来想去，突然发现由那三个等式竟然已经可以把a,b,c,d确定下来，结果原来这题是错题。

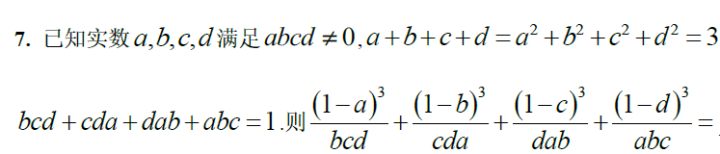
记 $p=a+b+c$, $q=ab+bc+ca$, $r=abc$，则有
\[(a-b)^2(b-c)^2(c-a)^2=-27r^2+2(9pq-2p^3)r+p^2q^2-4q^3,\]
依题意有
\begin{align*}
p&=3-d, \\
q&=\frac{(a+b+c)^2-(a^2+b^2+c^2)}2=\frac{(3-d)^2-(3-d^2)}2=d^2-3d+3, \\
r&=1-(ab+bc+ca)d=1-(d^2-3d+3)d=(1-d)^3,
\end{align*}
将它们代入化简后得到
\[(a-b)^2(b-c)^2(c-a)^2=-d^2(1-d)^2(16d^2-40d+27),\]
易证 $16d^2-40d+27>0$，故此左边非负右边非正，所以只能两边都为零，即得 $d=0$ 或 $d=1$，而当 $d=1$ 时 $r=abc=0$，所以必定有 $abcd=0$。

更具体一些，方程组 $a+b+c+d=a^2+b^2+c^2+d^2=3$, $abc+bcd+cda+dab=1$ 的实数解为 $a=b=c=1$, $d=0$ 及其轮换，共四组。

血狼王

kk，说不定题目就是这个意思

kuing

回复 2# 血狼王

他题目一开始就写 $abcd\ne0$，要是他本来就知道上面这些的话还会那样写吗？

血狼王

回复 3# kuing


原来如此，当初把abcd不等于0那条去掉就对了·

游客

               

调整下条件数值，使得最后的2元方程有非零解，不知道出题目的人怎么调的数据。