|
|
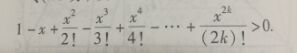
\[记f_n(x)=1-x+\cdots +(-1)^n\frac{x^n}{n!}\]
n=2时,成立
假设$n=2k,k\ge1$有$f_n(x)\ge 0$成立.
而$f'_{2k+1}(x)=-f_{2k}(x)<0$,说明$f_{2k+1}(x)$为减函数,$f_{2k+1}(0)>0,f_{2k+1}(2k+1)<0$,可得$f_{2k+1}(x)=0$有唯一零点,不妨设零点为x=t.
$n=2k+2$时,$f''_{2k+2}(x)=f_{2k}(x)>0$,说明$f_{2k+2}(x)$图象下凸.
此时$f_{2k+2}(x)$的最小值为$f_{2k+2}(t)=f_{2k+1}(t)+\frac{x^{2k+2}}{(2k+2)!}=0+\frac{x^{2k+2}}{(2k+2)!}>0$
...完. |
|