传令兵的轨迹

三尺水

速度恒定的传令兵在直径两公里，匀速前进的圆队伍尾，绕队伍跑一周回到队伍尾。队伍刚好走了两公里。求传令兵走的路径……传令兵开始在原点，队伍方程开始是x^2+(y-1)^2=1，向着y正方向匀速运动。
圆环直线匀速运动，点贴圆环运动，但是相对地面速度大小不变，方向是要求的

isee

看了两遍题，看不懂，放弃

战巡

明摆着该丢掉的题

一没说队伍是否直线前进，二没说传令兵相对队伍的环绕轨道如何（不一定要紧贴队伍边缘环绕，大可以绕更大的圈），这还做个屁？
“速度恒定”的传令兵这种表述也有严重问题，速度是带方向的，速度恒定意味着传令兵只能走直线，还绕个鬼？必须表述为“速率恒定”

想考摆线你弄个硬币滚转就完事了，弄这么复杂干啥？

三尺水

回复 3# 战巡
圆环直线前进，点贴圆环运动，点速度大小固定，方向让你求的，肯定不是摆线，别骄傲，这是我做过最简单的轨迹题

三尺水

回复 2# isee
圆环直线匀速运动，点贴圆环运动，点相对地面速度大小不变，但是方向是变的

战巡

回复 4# 三尺水

这么一说你之前的表述就又多了一个漏洞，你没有说过传令兵的速率是相对地面恒定还是相对队伍恒定，如果是相对队伍恒定就是摆线

三尺水

回复 6# 战巡

兵在地上跑……否则不符合逻辑。此问题数学方法有点难想

战巡

回复 7# 三尺水

没啥不合逻辑的，变速跑又不是很难

这个问题也并不难想，但计算烦人

令轨迹为参数方程$x(t),y(t)$，传令兵速度$v$为定值，队伍速度为$1$方便计算
有
\[\begin{cases} x'(t)^2+y'(t)^2=v^2\\x(t)^2+(y(t)-1-t)^2=1\end{cases}\]
对二式可得
\[t=\begin{cases}y(t)-\sqrt{1-x(t)^2}-1\\y(t)+\sqrt{1-y(t)^2}-1\end{cases}\]
\[1=\begin{cases}y'(t)-\frac{x(t)x'(t)}{\sqrt{1-x(t)^2}}\\y'(t)+\frac{x(t)x'(t)}{\sqrt{1-x(t)^2}}\end{cases}\]
以第一个为例
\[(\frac{1}{dt})^2=(dy-\frac{xdx}{\sqrt{1-x^2}})^2=\frac{(dx)^2+(dy)^2}{v^2}\]
\[(y'(x)-\frac{x}{\sqrt{1-x^2}})^2v^2=1+y'(x)^2\]
\[y'(x)=\begin{cases}\frac{1}{v^2-1}(\frac{v^2x}{\sqrt{1-x^2}}-\frac{\sqrt{v^2-1+x^2}}{\sqrt{1-x^2}})\\ \frac{1}{v^2-1}(\frac{v^2x}{\sqrt{1-x^2}}+\frac{\sqrt{v^2-1+x^2}}{\sqrt{1-x^2}})\end{cases}\]
然后，看好上下限，对其积分可得$y(x)$，再算出另外几段，对接在一起，最后得到轨迹，然后根据最终点的位置消掉$v$
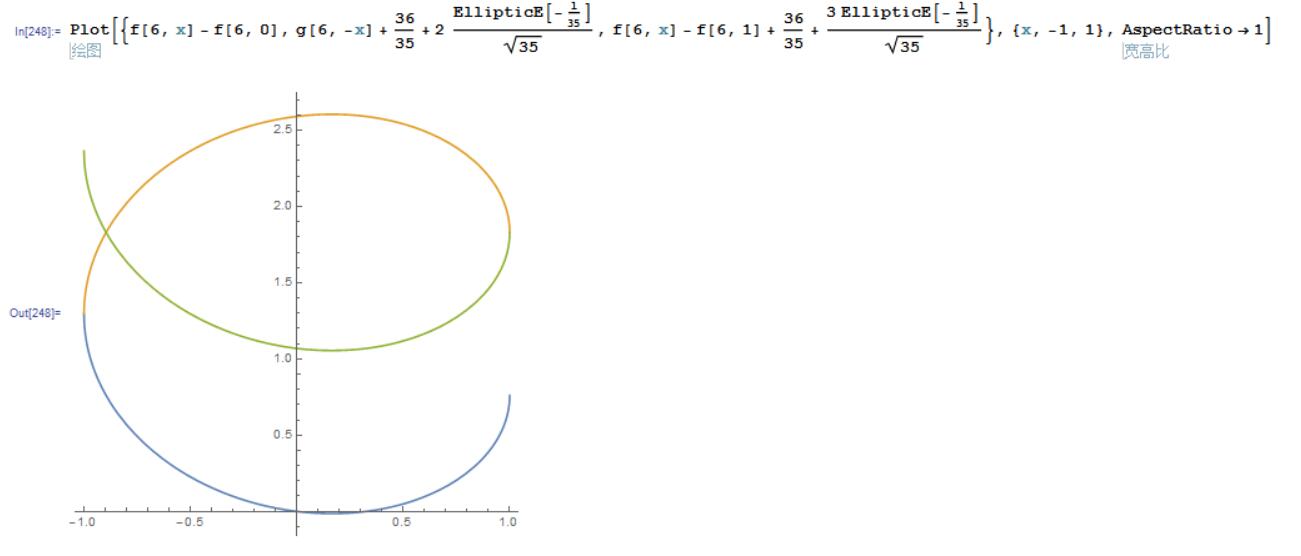
我这给你画了个大概的图，不过我懒得去消$v$，随便看看就好

三尺水

回复 8# 战巡


    速度等于队伍速度的3.36807倍